SOLUTION: Let f(x,y)=(x^2+2y^2)/ (x+y) if (x,y)otherthan(0,0) 0 otherwise Then the directional derivative of f at (0, 0) along u = (1, 1) is

Algebra ->  Finance -> SOLUTION: Let f(x,y)=(x^2+2y^2)/ (x+y) if (x,y)otherthan(0,0) 0 otherwise Then the directional derivative of f at (0, 0) along u = (1, 1) is      Log On


   

Question 1106994: Let
f(x,y)=(x^2+2y^2)/
(x+y) if (x,y)otherthan(0,0)
0 otherwise

Then the directional derivative of f at (0, 0) along u = (1, 1) is
Found 2 solutions by Fombitz, ikleyn:
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
Since the function is not defined at (0,0) then the directional derivative does not exist at (0,0).

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
If "s" is the parameter on the straight line x = y along the vector (1,1), then we have  


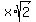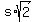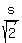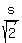    s = x%2Asqrt%282%29, y = s%2Asqrt%282%29,   or, equivalently,  x = s%2Fsqrt%282%29,  y = s%2Fsqrt%282%29.


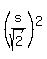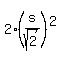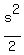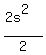Therefore, the numerator is x%5E2 + 2y%5E2 = %28s%2Fsqrt%282%29%29%5E2 + 2%2A%28s%2Fsqrt%282%29%29%5E2 = s%5E2%2F2 + %282s%5E2%29%2F2%29 = %283s%5E2%29%2F2,  


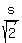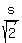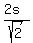while the denominator is x + y = s%2Fsqrt%282%29 + s%2Fsqrt%282%29 = %282s%29%2Fsqrt%282%29.


Then the ratio itself is

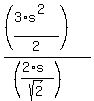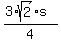f(x,y) = f(s) = %28%28%283%2As%5E2%29%2F2%29%29%2F%28%28%282%2As%29%2Fsqrt%282%29%29%29 = %283%2Asqrt%282%29%2As%29%2F4.


Thus the function f(s) is LINEAR on s along this direction, and is zero at  x= y= 0= s by the definition, which is consistent with the linear behavior.


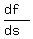So (and therefore), the derivative  %28df%29%2F%28ds%29  DOES EXIST  and is equal to %283%2Asqrt%282%29%29%2F4.

---------------------
To avoid misunderstanding, let me note (highlight/underline) that for the given function the derivative "along a direction"
DEPENDS on direction, so the function f(x,y) is NOT differentiate at (0,0) in the classic sense as a function of two variables.

It is ONLY differentiate "along a direction", and is a classic example of such a function.