Question 1105587: A, B, C, and D, are distinct digits, and 4(AAB) = CDA. If C is less than d, find the sum of a +b+c+d
Answer by ikleyn(52799)   (Show Source):
You can put this solution on YOUR website! .
A, B, C, and D, are distinct digits, and 4(AAB) = CDA. If C is less than d, find the sum of a +b+c+d
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
1. From 4*(AAB) = CDA, it follows that A is an even number/digit different from zero and not more than 2.
It leaves only one possibility for A: A = 2.
2. Since A = 2, it leaves only two possibilities for C: C= 8 or C= 9.
Since, in addition, C is less than D, it implies that C= 8 and D= 9.
3. Then CDA = 892, and it implies that AAB = 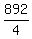 = 223.
4. Thus we just found that AAB = 223, CDA = 892,
A= 2, B= 3, C= 8, D= 9.
Then A + B + C + D = 2 + 3 + 8 + 9 = 22.
Answer. A + B + C + D = 22.
|
|
|
