Question 1104775: fonction of composition (Fog)(x)=1/x^2 and g(x)= 2x+1
find f(x)=?
thanks
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! fog(x) = 1/x^2
g(x) = 2x+1
find f(x) .....
you start with g(x) and wind up with fog(x).
fog(x) means f(g(x)) which means f(2x+1).
therefore, you have f(2x+1) = 1/x^2
you are looking for something that happens to 2x+1 that makes the result equal to 1/x^2.
i played around with it for a while and then decided to figure out what happens to (2x+1)^2 and how i can make the result equal to x^2.
so i squared (2x+1) and got 4x^2 + 4x + 1.
i needed to get rid of the 4x, so i subtracted 2 * (2x+1) from it to get:
4x^2 + 4x + 1 - 2 * (2x+1) = 4x^2 + 4x + 1 -4x - 2 which simplifed to 4x^2 - 1.
i then added 1 to it to get 4x^2.
i then divided it by 4 to get x^2.
i wound up with 4 / ((2x+1)^2 - 2*(2x+1) + 1)
i then replaced 2x+1 with x and got 4 / (x^2 - 2x + 1).
that became f(x).
to confirm i did the right thing, i then went through the process of converting f(x) and g(x) to fog(x).
i started with f(x) = 4/(x^2 - 2x + 1) and g(x) = 2x + 1
fog(x) is equal to f(g(x)) which is equal to f(2x+1).
this means replace x with 2x + 1 in f(x).
since f(x) = 4 / (x^2 - 2x + 1), then replacing x with (2x+1) results in fog(x) = 4 / ((2x+1)^2 - 2*(2x+1) + 1).
expanding this, i got fog(x) = 4 / (4x^2 + 4x + 1 - 4x - 2 + 1)
simplifying this, i got fog(x) = 4 / 4x^2.
simplifying further, i got fog(x) = 1/x^2.
looks like i got it right.
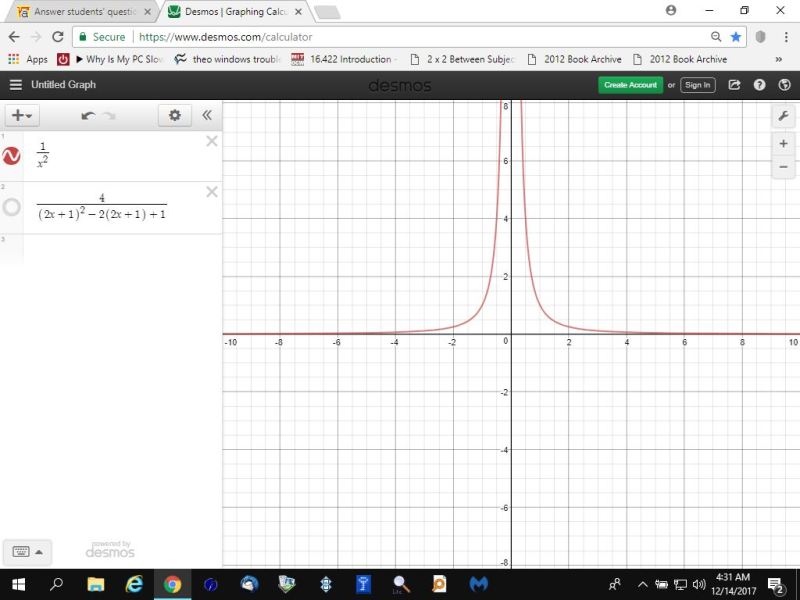
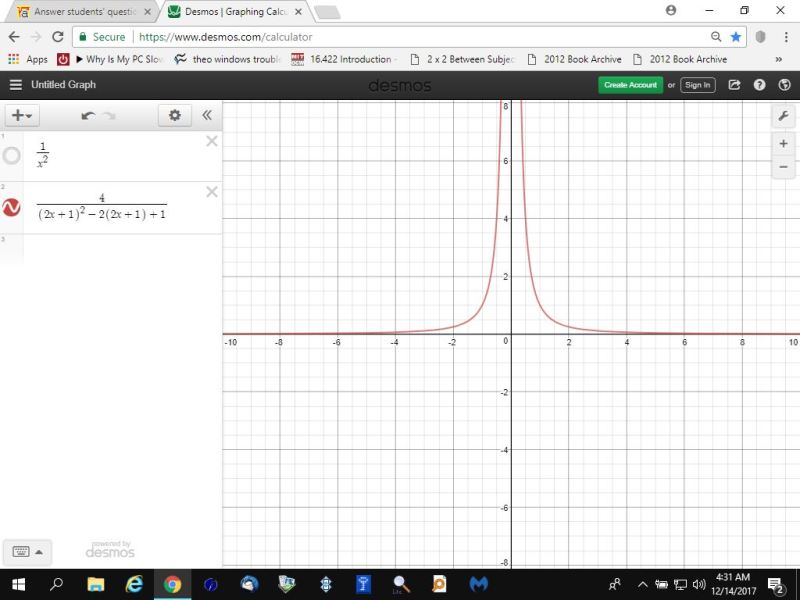
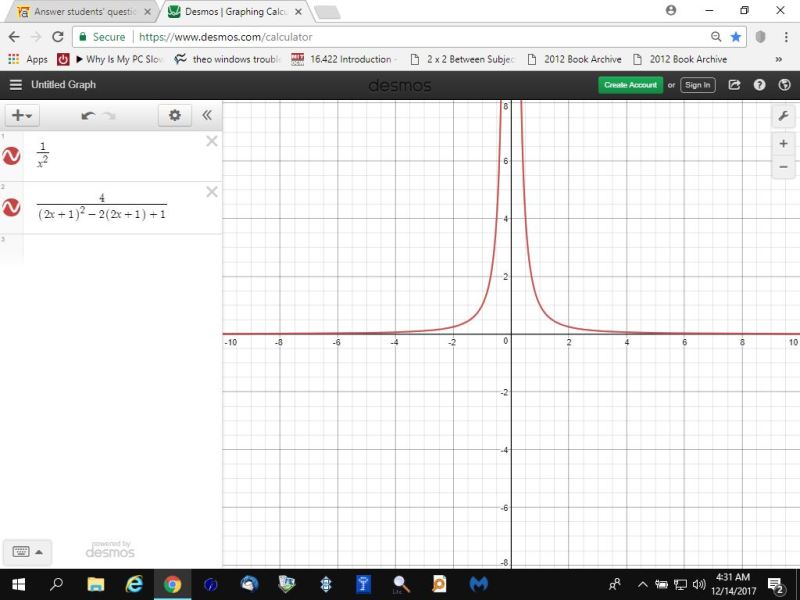
i went further to graph both 1/x^2 and 4/((2x+1)^2 - 2*(2x+1) + 1).
the graphs are identical, indicating that the equations are equivalent.
my graphs are shown below.
the first graph shows 1/x^2.
the second graph shows 4 / ((2x+1)^2 - 2*(2x+1) + 1)
the third graph show them both together, resulting in the same graph, indicating the equations are equivalent to each other.
the little circles on the left tell you which equation is being graphed.
if they're filled in with the color of the graph, that graph is showing.
you can see when they're both being graphed together, their graph is identical, confirming the equations are equivalent to each other.
your solution is f(x) = 4 / (x^2 - 2x + 1)
|
|
|