Question 1103131: The perimeter of a right triangle is 60 inches and the length of the altitude to the hypotenuse is 12 inches. How many square inches are in the area of the triangle?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
This looks to be one of those problems that is more easily solved by trial and error than by formal algebra; every algebraic approach I looked at resulted in an equation that could only be solved using a graphing calculator.
So what do we know about the altitude to the hypotenuse of a right triangle?
We know it divides the right triangle into two other right triangles, both of which are similar to the original triangle.
And we know that those similar triangles can be used to show that the length of the altitude to the hypotenuse is the geometric mean of the lengths of the two segments of the hypotenuse.
So let the right triangle be ABC, with right angle at A; and let D on hypotenuse BC be the foot of the altitude. Then  . .
Now let's hope that the numbers in the problem are "nice" -- so let's choose nice numbers for the lengths of BD and DC such that BD*DC = 144. There are several choices; but one that makes the problem easy to solve from here is 9 and 16.
With BD=9 and AD=12, AB is 15; with CD=16 and AD=12, AC is 20.
And then the perimeter of ABC is 15+20+25 = 60, which is what we wanted.
So AB=15 and AC=20 are the legs of the right triangle; so the area of the triangle is  . .
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The perimeter of a right triangle is 60 inches and the length of the altitude to the hypotenuse is 12 inches.
How many square inches are in the area of the triangle?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x and y be the legs lengths.
Then the hypotenuse is  .
The "perimeter" equation is .
The "perimeter" equation is
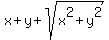 = 60, (1)
which implies = 60, (1)
which implies
 = 60 - (x+y), = 60 - (x+y),
 = = 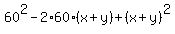 , ,
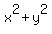 = = 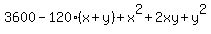 ,
2xy = 120*(x+y) - 3600,
xy = 60*(x+y) - 1800. (2)
From the other side, you have this equation expressing the area of the right-angled triangle ,
2xy = 120*(x+y) - 3600,
xy = 60*(x+y) - 1800. (2)
From the other side, you have this equation expressing the area of the right-angled triangle
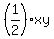 = = 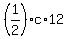 ,
which gives
xy = ,
which gives
xy = 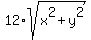 . (3)
In this equation, replace . (3)
In this equation, replace  in the right side by [60 - (x+y)], based on (2).
You will get instead of (3)
xy = 12*(60 - (x+y)). (4)
Now compare equations (2) and (4). Their left sides are identical; hence, right sides are equal:
60*(x+y) - 1800 = 12*(60 - (x+y)).
It implies 60*(x+y) + 12*(x+y) = 12*60 + 1800, or 72*(x+y) = 2520, and then x+y = in the right side by [60 - (x+y)], based on (2).
You will get instead of (3)
xy = 12*(60 - (x+y)). (4)
Now compare equations (2) and (4). Their left sides are identical; hence, right sides are equal:
60*(x+y) - 1800 = 12*(60 - (x+y)).
It implies 60*(x+y) + 12*(x+y) = 12*60 + 1800, or 72*(x+y) = 2520, and then x+y = 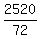 = 35.
Thus we found that the sum of the leg lengths is 35 inches.
Then the hypotenuse is 60 - 35 = 25 inches (from the condition on the perimeter),
and the area of the triangle, which is under the question, is = 35.
Thus we found that the sum of the leg lengths is 35 inches.
Then the hypotenuse is 60 - 35 = 25 inches (from the condition on the perimeter),
and the area of the triangle, which is under the question, is 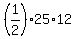 = 25*6 = 150 square inches. = 25*6 = 150 square inches.
SOLVED.
----------------
By knowing that x+y = 35 and x^2 + y^2 = 25^2, it is easy to find the values of x and y individually.
At this level, it is just standard exercise in solving quadratic equations, and I leave it to you.
|
|
|