Question 1102166: You sign up to volunteer every fifth Sunday when one occurs. If you choose a typical thirty one day month, what is the probability that you will be needed on a fifth Sunday? Write your probability in a simplified fraction.
Found 2 solutions by Lightning_Fast, richwmiller:
Answer by Lightning_Fast(78)   (Show Source): (Show Source):
You can put this solution on YOUR website! Well, assuming the thirty day month starts on a Sunday, there will be four Sundays.
When you say every other Sunday, you are skipping one sunday, then volunteering one sunday, then skipping one sunday, then volunteering on sunday. You are volunteering for 2/4 sundays, or 1/2.
How about skipping every third Sunday? You skip one Sunday, then skip again, then volunteer. Here, you Volunteer for 1/3 Sunday.
When you volunteer for every fifth sunday, you will have a 1/5 chance of going to volunteer per sunday, or per week.
We can write this as a ratio.

But we have four weeks, or four sundays in a month, so we multiply the numerator and the denominator by four and obtain.
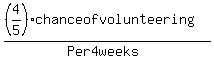
Your provability is 4/5 chance of volunteering for any given month.
Answer by richwmiller(17219)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are 7 months with 31 days
jan mar may jul aug oct dec
There are three starting dates when there are 5 Sundays
If the 1st is a Sunday 1,8,15,22,29
If the 2nd is a Sunday 2,9,16,23,30
If the 3rd is a Sunday 3,10,17,24,31
If you choose a typical 31 day month, what is the probability that you will be needed on a fifth Sunday?
So we have already chosen the 7 eligible months.
In the eligible months, the probability is 3 out of 7 starting days will result in a fifth Sunday.
Write your probability in a simplified fraction.
3/7
|
|
|