Question 1101300: iceman has enclosed one of his mortal enemies in a cube of ice. it is melting uniformly with the volume decreasing by 3 cubic feet per sec how fast is the surface area decreasing when the cubes edge is 5 ft?
i got lost when they are asking about the surface area. Thanks for helping out!
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! AS A CALCULUS PROBLEM:
 = length of the edge, in ft
 = surface area of the cube, in square feet
 = volume of the cube, in cubic feet
 = time, in seconds
,  , and  are functions of .
We know the rate of change of with ,  .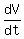
If we figure out the relations among the derivatives of those functions,
we can calculate the rate of change for and .
If  , then 
Substituting that into the expression for  ,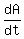
When  ,  .
When the cube's edge is 5 ft,
the surface area is decreasing at a rate of
 square feet per second.
OTHER OPTIONS:
As a good approximation, calculate the average rate of area decrease
between 0.01 seconds before the cube edge measures 5 ft
and 0.01 seconds after the cube edge measures 5 ft.
When the edge measures 5 ft, the volume, in cubic feet, is
 .
0.01 seconds before that, the volume, in cubic feet, is
 ,
the edge length, in feet, is  ,
and the surface area, in square feet, is
 .
0.01 seconds after the edge measures 5 ft, the volume, in cubic feet, is
 ,
the edge length, in feet, is  ,
and the surface area, in square feet, is
 .
So, over the course of 0.02 seconds,
the surface area decrease, in square feet, is
 ,
making the rate of decrease, in square feet per second,
 .
|
|
|
