Question 1095295: For the polynomial, state (a)the degree (b)whether it is odd, even or neither (c)end behavior (d)number of zeroes and multiplicities if any (e)graph the polynomial function.
f(x)=x^4-9x^2
Answer by htmentor(1343)   (Show Source):
You can put this solution on YOUR website! a) The degree is 4 since the leading term is x^4.
b) The function is even if f(x) = f(-x).
Since both terms have even exponents, f(-x) is equal to f(x), so the function is even.
c) For large x, or large negative x, f(x) ~ x^4, so the function grows without bounds, i.e. f(x) -> infinity
d) x^4 - 9x^2 -> x^2(x^2 - 9) -> x^2(x+3)(x-3), so the zeros are 3, -3 (mult. 1) and 0 (mult. 2)
e)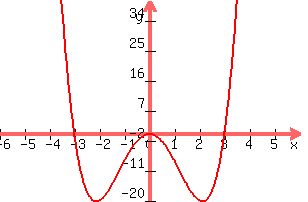 
|
|
|
