SOLUTION: The probability that a bomb dropped from a plan over bridge will hit the bridge is 1/5 two bombs are enough to destroy the bridge .if 6 bombs are dropped on the bridge find the pro

Algebra ->  Finance -> SOLUTION: The probability that a bomb dropped from a plan over bridge will hit the bridge is 1/5 two bombs are enough to destroy the bridge .if 6 bombs are dropped on the bridge find the pro      Log On


   

Question 1090258: The probability that a bomb dropped from a plan over bridge will hit the bridge is 1/5 two bombs are enough to destroy the bridge .if 6 bombs are dropped on the bridge find the probability that the bridge will be destroyed.
Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


This is a binomial probability problem. We can represent the fact that each bomb has a 1/5 probability of hitting (Y = yes) the bridge and a 4/5 probability of not hitting the bridge (N = no) with a "probability vector":


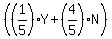
%28%281%2F5%29%2AY%2B%284%2F5%29%2AN%29


Then the probabilities of hitting the bridge with 0, 1, ..., 5, or 6 of the bombs will be the coefficients of the expansion of


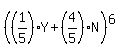
%28%281%2F5%29Y%2B%284%2F5%29N%29%5E6


Use the binomial theorem to expand that expression and find the appropriate coefficients. Since the bridge will be destroyed if it is hit by 2, 3, 4, 5, or 6 bombs, you could solve the problem by calculating those 5 coefficients. But it is much faster to calculate the probability that the bridge is NOT destroyed by calculating the probabilities that the bridge is hit by either 0 or 1 bomb; then the probability that the bridge is destroyed is 1 minus that probability.


P%280%29=C%286%2C0%29%281%2F5%29%5E0%284%2F5%29%5E6=0.26214
P%281%29=C%286%2C1%29%281%2F5%29%5E1%284%2F5%29%5E5=0.39322
The probability that the bridge will be destroyed is
1-%280.26214%2B.39322%29+=+0.34464