Question 1084270: It is tempting to try to solve an inequality like an equation. For instance, we might try to solve 1<3/x
by multiplying both sides by x, to get x < 3, so the solution would be (-∞ ,3)
But thatís wrong; for example, x = -1 lies in this interval but does not satisfy the original inequality. Explain why this method does not work. In addition, solve the inequality correctly. Please be sure to explain your reasoning!
Found 3 solutions by MathLover1, KMST, MathTherapy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! With an equation, multiplying both sides by a number other than zero gives you an equivalent equation, with exactly the same solutions. Multiplying times zero gives you 0=0, which in most cases would have more solutions than the original equation. For equations, if we multiply times an expression involving x, we could be gaining solutions that do not work for the original equation (extraneous solutions).
For inequalities, it gets more complicates, not only we have to worry about factors that could be zero. we also have to worry about if a factor is negative or positive.
For an inequality, multiplying times a non-zero factor both sides of the inequality sign, and keeping the inequality sign as is, will give you an equivalent inequality only if the factor is positive.
For example 1<2 , and multiplying times 3, we get 3<6, which is equally true.
However, if we multiply times -5 both sides, we would get -5 and -10,
and we know that -5 > -10.
For an inequality, multiplying times a negative number both sides of the inequality sign, and turning around the inequality sign, will give you an equivalent inequality.
With 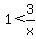 we know that we know that  is not a solution. is not a solution.
We could multiply times  and solve and solve 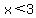 , but that means we are assuming , but that means we are assuming 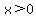 . .
Could it be that 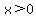 ? Assuming ? Assuming 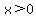 , we could multiply both sides times x, and get the equivalent equation , we could multiply both sides times x, and get the equivalent equation 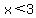 , which does not quite contradict the assumption that , which does not quite contradict the assumption that 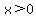 . So, we know that x values such that . So, we know that x values such that 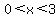 are solutions of are solutions of 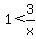 . .
Could it be that there are any solutions with  ? Assuming ? Assuming  , an equivalent inequality would be , an equivalent inequality would be  , which is not true for any , which is not true for any  . So, there are no other solutions. . So, there are no other solutions.
Answer by MathTherapy(10559)   (Show Source): (Show Source):
You can put this solution on YOUR website! It is tempting to try to solve an inequality like an equation. For instance, we might try to solve 1<3/x
by multiplying both sides by x, to get x < 3, so the solution would be (-∞ ,3)
But thatís wrong; for example, x = -1 lies in this interval but does not satisfy the original inequality. Explain why this method does not work. In addition, solve the inequality correctly. Please be sure to explain your reasoning!
When SOLVING INEQUALITIES, there are specific steps. One of the most important steps is to solve the inequality as you would, an equation.
Before doing any of that though you need to observe the fraction to the right of the INEQUALITY. It's 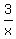 . .
Right away, it's realized that x CANNOT = 0, or  . The fact that . The fact that  makes 0 a CRITICAL VALUE. makes 0 a CRITICAL VALUE.
Solving the inequality the way you would an equation gives you a value of x = 3. Now, we have TWO (2) critical values, namely: 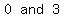
Place these TWO (2) critical values on a NUMBER LINE and you'll notice that that are 3 intervals that MIGHT INCLUDE values for x: 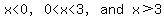 . .
You now use values WITHIN those INTERVALS to determine which values within which INTERVAL(S) satisfies(y) the INEQUALITY.
For x < 0, choose a value as such: one that's < 0. This VALUE WILL NOT satisfy the INEQUALITY.
For 0 < x < 3, choose a value as such: one that's > 0 but < 3. This VALUE WILL satisfy the INEQUALITY.
For x > 0, choose a value as such: one that's > 0. This VALUE WILL NOT satisfy the INEQUALITY.
Therefore, only ONE (1) interval contains values that SATISFY the inequality: 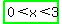
|
|
|