SOLUTION: Carlo and Anita make mailboxes and toys in their craft shop near Lincoln. Each mailbox requires 3 hours of work from Carlo and 4 hours from Anita. Each toy requires 2 hours of work

Algebra ->  Finance -> SOLUTION: Carlo and Anita make mailboxes and toys in their craft shop near Lincoln. Each mailbox requires 3 hours of work from Carlo and 4 hours from Anita. Each toy requires 2 hours of work      Log On


   

Question 1066773: Carlo and Anita make mailboxes and toys in their craft shop near Lincoln. Each mailbox requires 3 hours of work from Carlo and 4 hours from Anita. Each toy requires 2 hours of work from Carlo and 4 hours from Anita. Carlo cannot work more than 18 hours per week and Anita cannot work more than 32 hours per week. If each mailbox sells for $11 and each toy sells for $12​, then how many of each should they make to maximize their​ revenue? What is their maximum​ revenue?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
                  HOURS 1 mailbox        HOURS 1 toy     TIME LIMIT
         --------------------------------------------------------------
        Carlo        3                     2                  18
        Anita        4                     4                  32

Let x be how many mailboxes
Let y be how many toys

Carlo and Anita have these time limits:
system%283x%2B2y%3C=18%2C4x%2B4y%3C=32%29
In addition to that,
system%28x%3E0%2Cy%3E0%29

Here is the revenue R for x mailboxes and y toys:
R=11x%2B12y

You are likely to find the best R at one of the corners of the figure bounded by system%283x%2B2y%3C=18%2C4x%2B4y%3C=32%2Cx%3E0%2Cy%3E0%29. (Graph not shown here)

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
Carlo and Anita make mailboxes and toys in their craft shop near Lincoln.
Each mailbox requires 3 hours of work from Carlo and 4 hours from Anita.
Each toy requires 2 hours of work from Carlo and 4 hours from Anita.
Carlo cannot work more than 18 hours per week and
Anita cannot work more than 32 hours per week.
If each mailbox sells for $11 and each toy sells for $12,
then how many of each should they make to maximize their revenue? What is their maximum revenue?
~~~~~~~~~~~~~~~~~~~~

I re-formatted the input to provide the maximal readability (!!) 

The question is: how many mailboxes (X) and how many toys (Y) should be produced to maximize the revenue $11*X + $12*Y
under these restrictions:

3X + 2Y <= 18     (1)     (Carlo restricted by 18 hours per week) and
4X + 4Y <= 32     (2)     (Anita restricted by 32 hours per week).

In other words, you must maximize the objective function (revenue) 

R(X,Y) = 11X + 12Y

over the domain on the plot below, which is  a quadrilateral in the first quadrant (X >= 0,  Y >= 0) restricted 
by the red and the green lines.





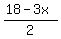Plots y = %2818-3x%29%2F2  (red) and y = %2832-4x%29%2F4 (green)



The method of linear programming says:

    1) Take the vertices of this quadrilateral

        (x1,Y1) = (0,8)   (green line Y-intercept)
        (x2,Y2) = (6,0)   (red line X-intercept)
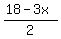        (x3,Y3) = (2,6)   (intersection point of the straight lines Y = %2818-3x%29%2F2 and Y = %2832-4x%29%2F4 )

    2) Calculate the objective function at these points

        R(X1,Y1) = 11*0 + 12*8 = 96;

        R(X2,Y2) = 11*6 + 12*0 = 66;

        R(X3,Y3) = 11*2 + 12*6 = 94.


    3) Then select one of these point where the objective function is maximal - In our case this point is (X1,Y1) = (0,8)


    4) This point gives your optimal solution X = 0 mailboxes and Y = 8 toys.


If they follow this optimal solution, their weekly revenue will be MAXIMAL, $96.

Solved.