Question 1054861: Is this true or false? Please check image
Statement: http://s11.postimg.org/79zhn751v/image.png
x - 1 = 0, x = 1
Undefined: x ≠ 1, x < 1, x > 1
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i'm not exactly sure what you are looking for.
your equation is y = (x^2 + x - 2) / (x - 1)
when x = 1, the function is undefined because you can't divide by 0 and get a real number.
therefore, the function is good for all values of x except when x = 1.
there is not an asymptote to this equation because the denominator cancels out when you factor the numerator.
if you factor (x^2 + x - 2), you get (x + 2) * (x - 1).
the equation bec0omes y = (x + 2) * (x - 1) / (x - 1).
the (x - 1) in the numerator and the denominator cancel out and you are left with y = x + 2.
when you graph the equation, that's what you see.
here's the graph.
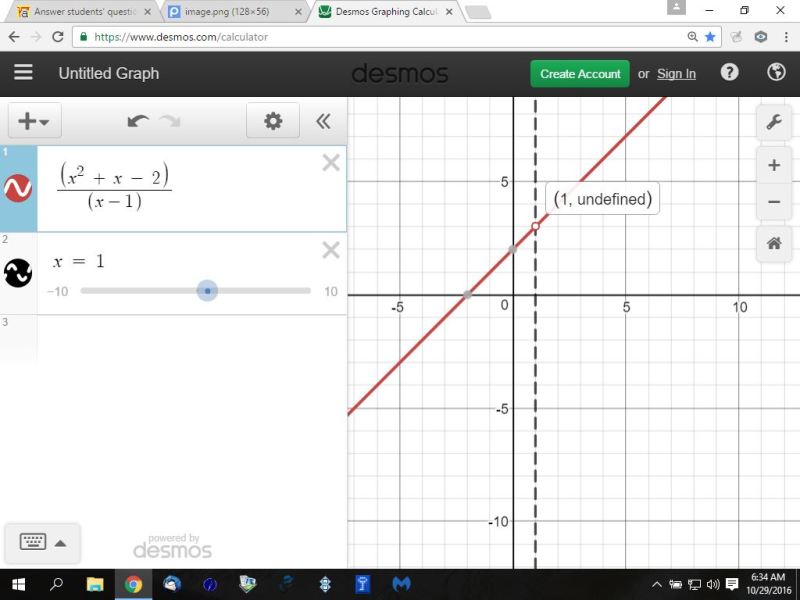
as you can see, the value of the function is undefined when x = 1.
for all other values of x, the function is valid.
now to your statements that i don't completely understand what you mean by them.
x - 1 = 0, x = 1
Undefined: x ≠ 1, x < 1, x > 1
the function is defined when x is not equal to 1.
if the statement is saying that the function is undefined when x is not equal to 1, then the statement is false.
|
|
|