Question 1041919: A manufacturing company receives orders for engines from two assembly plants. Plant I needs at least 45 engines, and plant II needs at least 32 engines. The company can send at most 120 engines to these assembly plants. It costs $30 per engine to ship to plant I and $40 per engine to ship to plant II. Plant I gives the manufacturing company $20 in rebates toward its products for each engine they buy, while plant II gives similar $10 rebates. The manufacturer estimates that they need at least $1500 in rebates to cover products they plan to buy from the two plants. How many engines should be shipped to each plant to minimize shipping costs? What is the minimum cost?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your objective function is to minimize the cost.
set x equal to the number of engines shipped to plant I.
set y equal to the number of engines shipped to plant II.
total cost = 30x + 40y
that's the function you want to minimize.
it costs 30 dollars to ship 1 engine to plant I.
it costs 40 dollars to ship 1 engine to plant II.
set c = total cost.
your objective function is c = 30x + 40y.
your constraints are:
x >= 45
y >= 32
this means you need to ship at least 45 engines to plant I and at least 32 engines to plant II.
x >= 0
y >= 0
this means that the number of engines shipped has to be equal to or greater than 0.
20x + 10y >= 1500
this means that the total rebates provided by the assembly plants has to be greater than or equal to 1500.
x + y < = 120
this means that the total number of engines that can be shipped has to be less than or equal to 120.
summarize your formulas:
objective function:
c = 30x + 40y
constraints:
x + y <= 120
x >= 45
y >= 32
20x + 10y >= 1500
graph the constraint equations and then shade the areas on the graph that satisfy the inequalities.
this is what my graph looks like.
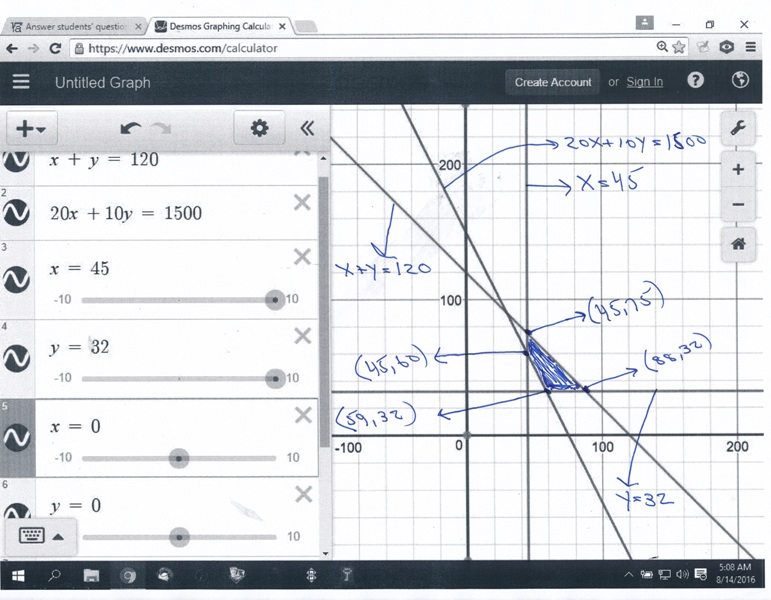
i graphed the equations.
i then shaded the areas that satisfied the inequalities.
then you need to find the corner points of the shaded area.
those are:
(45,75)
(45,60)
(59,32)
(88,32)
you then analyze the objective function at those corner points.
objective function is c = 30x + 40y
at (45,75), you get 30*45 + 40*75 = 4350
at (45,60), you get 30*45 + 40*60 = 3750
at (59,32), you get 30*59 + 40*32 = 3050
at (88,32), you get 30*88 + 40*32 = 3920
your minimum cost is when x = 59 and y = 32.
your minimum cost is 3050.
all your constraints need to be satisfied as well.
x + y <= 120 becomes 59 + 32 <= 120 which becomes 91 <= 120 which is true.
x >= 45 becomes 59 >= 45 which is true.
y >= 32 becomes 32 >= 32 which is true.
x and y >= 0 are automatically satisfied when x >= 45 and y >= 32.
20x + 10y >= 1500 becomes 59*20 + 32*10 >= 1500 which becomes 1180 + 320 >= 1500 which becomes 1500 >= 1500 which is true.
all the constraints are satisfied.
your solution is that the minimum cost is 3050.
|
|
|