Question 1034317: Please help me solve this question
Solve the system; logx base a.log ( xyz ) base a = 48
Logy base a.log ( xyz ) base a = 12, a > 0, a is not = to 1
Logz base a.log ( xyz ) base a = 84
Answer by ikleyn(52943)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Please help me solve this question
Solve the system; logx base a.log ( xyz ) base a = 48,
Logy base a.log ( xyz ) base a = 12,
Logz base a.log ( xyz ) base a = 84,
a > 0, a is not = to 1
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
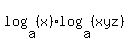 = =  , (1) , (1)
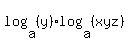 = =  , (2) , (2)
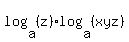 = =  . (3)
Add (1), (2) and (3) (both sides). You will get . (3)
Add (1), (2) and (3) (both sides). You will get
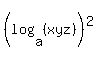 = 48 + 12 + 84 = 144.
Hence, = 48 + 12 + 84 = 144.
Hence, 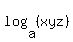 = +/- 12.
Now, consider two cases.
a) = +/- 12.
Now, consider two cases.
a) 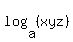 = + 12.
Then = + 12.
Then 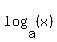 = = 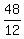 = 4 ---> x = = 4 ---> x = 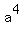 , ,
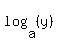 = =  = 1 ---> y = = 1 ---> y =  , ,
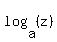 = = 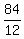 = 7 ---> z = = 7 ---> z =  .
b) .
b) 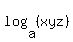 = - 12.
Then = - 12.
Then 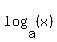 = = 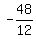 = -4 ---> x = = -4 ---> x = 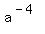 , ,
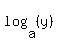 = = 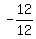 = -1 ---> y = = -1 ---> y =  , ,
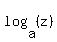 = = 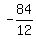 = -7 ---> z = = -7 ---> z =  .
Thus you have two solutions (or two sets of solutions). .
Thus you have two solutions (or two sets of solutions).
|
|
|