.
A square has a side length of 9 cm. the midpoints of each side is connected to form another square.
This process continues indefinitely. Consider each square separately. Find the
(a). Total perimeter of all the squares.
The very first square has the perimeter of 4*9 = 36 cm.
Each next, (n+1)-th square, has the perimeter 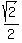 of that of n-th square.
So, the sequence of perimeters is an infinite geometric progression with the first term 36 and the common ratio
of that of n-th square.
So, the sequence of perimeters is an infinite geometric progression with the first term 36 and the common ratio 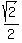 .
The sum of this progression is
.
The sum of this progression is  =
= 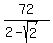 =
= 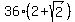 cm.
cm.
(b). total area of all the squares.
The very first square has the area of 9*9 = 81  .
Each next, (n+1)-th square, has the area half of that of n-th square.
So, the sequence of areas is an infinite geometric progression with the first term 81 and the common ratio
.
Each next, (n+1)-th square, has the area half of that of n-th square.
So, the sequence of areas is an infinite geometric progression with the first term 81 and the common ratio  .
The sum of this progression is
.
The sum of this progression is 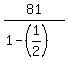 = 162
= 162  .
.