Question 1022074: I need help with this too:
Sketch the graph of y =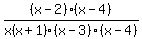 
Found 2 solutions by stanbon, Boreal:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! Sketch the graph of y = [(x - 2)(x - 4)]/[x(x + 1)(x - 3)(x - 4)]
------
Hole at x = 4 (no y-value there)
------------------
Vertical asymptotes at x = 0, x = -1 and x = 3
--------------------
End Behavior::
f(x) = x^2/x^4 = 1/x^2
f(x) goes to zero as x goes to +oo and as x goes to -oo
-----
With that information you should be able to sketch the graph.
--------------
-----------
Cheers,
Stan H.
-----------
Answer by Boreal(15235)  (Show Source):
You can put this solution on YOUR website! It has vertical asymptotes at -1,0,3, and a hole at 4, because the (x-4) divide out.
Then look at critical points on each side.
When x goes to - infinity, two minuses on top, 4 on the bottom, and it goes to 0 from the positive side. At x=2, the function is 0.
When x is between -1 and 0, (x+1) is positive, so the function is negative.
When x is greater than 0 and less than 2, the function is positive.
x is between 2 and 4 not inclusive, the function is negative.
When x is greater than 4, it goes to zero from the positive side, because all the terms are positive.
The reason the function goes to 0 when x goes to infinity is that there is an x^2 on top and an x^4 on the bottom as the highest power terms.
|
|
|
