Question 1010653: (1) f and g are functions on X={1,2,3} as f—{(1,2); (2,3); (3,1)) ; g=(1,2); (2,1); (3,3)}. Compute; fog and gof
(2) Let F, be the number of faces in G, where G is a connected planar simple graph with E edges and V vertices. Obtain an equation connecting F. E and V. Hence derive value(s) of F, E and V to form a graph such that the graph is a planar.
(3) Deduce the combination of n+1 element taken n-1 at a time denoted as C
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
(1) f and g are functions on X={1,2,3} as f—{(1,2); (2,3); (3,1)) ; g=(1,2); (2,1); (3,3)}. Compute; fog and gof
(2) Let F, be the number of faces in G, where G is a connected planar simple graph with E edges and V vertices. Obtain an equation connecting F. E and V. Hence derive value(s) of F, E and V to form a graph such that the graph is a planar.
(3) Deduce the combination of n+1 element taken n-1 at a time denoted as C
------------------------------------------------------------------------
(2) F - E + V = 1.
Draw any planar graph on a plane and check this formula.
It is the planar analog of the famous Euler's formula for the numbers of faces, edges and vertices of a polyhedron.
(3)  =  =  .
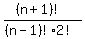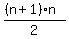See the lesson Introduction to Combinations in this site.
|
|
|
