SOLUTION: how do I solve this system of equations by substitution 5x+6y=32 12y-4x=8

Algebra ->  Expressions-with-variables -> SOLUTION: how do I solve this system of equations by substitution 5x+6y=32 12y-4x=8      Log On


   

Question 697656: how do I solve this system of equations by substitution
5x+6y=32
12y-4x=8
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
 5x + 6y = 32
12y - 4x =  8

Solve the second equation for x

12y - 4x = 8
     -4x = 8 - 12y

Divide every term by the coefficient of x, which is -4:

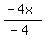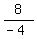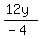     %28-4x%29%2F%28-4%29 = 8%2F%28-4%29 - %2812y%29%2F%28-4%29

       x = -2 - (-3y)
       x = -2 + 3y

Now substitute (-2 + 3y) for x in the other equation at
the top:


        5x + 6y = 32
5(-2 + 3y) + 6y = 32
 -10 + 15y + 6y = 32
      -10 + 21y = 32
            21y = 42
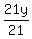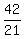            21y%2F21 = 42%2F21
              y = 2

Now go back to where you solved for x:

       x = -2 + 3y

and replace y by (2)

       x = -2 + 3(2)
       x = -2 + 6
       x = 4

So the solution is (x,y) = (4,2)

Checking the answer in the first equation:

     5x + 6y = 32
 5(4) + 6(2) = 32
     20 + 12 = 32
          32 = 32

Checking the answer in the second equation:

    12y - 4x = 8
12(2) - 4(4) = 8
     24 - 16 = 8
           8 = 8

So (x,y) = (4,2) is correct because it checks in
BOTH equations.

Edwin