Question 43043: How do I solve each system by either elimination or substitution?
5x + 2y = 1
x - 3y = 7
My second problem is the same
y = 2x + 4
x - y = 11
Answer by aaaaaaaa(138)   (Show Source): (Show Source):
You can put this solution on YOUR website! I will solve only one of them. You have the other as an exercise. First, by substitution. We have:


We need to isolate x or y on one side of one equation. Let's try the second, which is easier since the coefficient of x is 1:
When we pass a number to the other side, it's sign is the inverse, so we pass 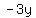 as as 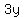 to get: to get:

The first expression is now solved, but with 7 + 3y in the place of x.

Distributive property:

Adding like terms:

Now, we have that  , substitute that into , substitute that into
 : :




Now, what would happen if we tried the first one in the beginning? We would pass 2y to the right side and the coefficient 5, getting:

And solving by substituting that into the second equation like above.
Now, by elimination:
When we have two equations, we can add the terms to make another true equation, for example:



Verify that the last equation is true. We have:


And so we want to get the same coefficient into at least one variable (with changed signs) so we can cancel it to 0. We can bring the oefficient of x in the second equation to -5 by multiplying all terms by -5 (and then  ), so let's do that: ), so let's do that:


Now, we add all terms, just like we did above:

Notice that 5x and -5x cancelled themselves out, leaving us a simple linear equation.



Plug in y in any of our equations now. Let's try the first,  . .





|
|
|