|
Question 126497: Please show me how to solve this problem ( it was a homework problem (1 complete problem) and I didn't know where to start). thanks!
200 Students
70 Students take English class
54 Students take Math class
45 Students take Social Studies
28 Students take English and Math
19 Students take English and Scial Studies
15 Students take Math and Scial Studies
10 Students take English, Math and Social Studies
1.) How many students take English
2.) How many Students take math only
3.) How many Students take English, social studies but not math
4.) How many students take math and social studies but not English class
5.) How many do not take any class.
Answer by marcsam823(57)   (Show Source):
You can put this solution on YOUR website! Since this problem contains several elements that are more easily tracked with a picture, I find the easiest way to solve it is with a Venn Diagram. Venn Diagrams are basically a series of overlapping circles that allow you to see all at once how your data relates. I can't draw Venn diagrams on this site, but if you'd like to learn more about them, go this site:
http://en.wikipedia.org/wiki/Venn_diagram and click the Examples hyperlink.
Question 1)
We are given that a total of 70 students take English class. These students can be divided into 4 groups:
a = Students who take English, Math and Social Studies
b = Students who take English and Social Studies only
c = Students who take English and Math only
d = Students who take English only
a + b + c + d = 70 = Total students taking English
1. The problem gives us  students who take all 3 classes. This is a good start, because it will help us solve for b and c
2. Solve for b:
The problem also tells us that 19 students take English and Social Studies. This can be a little confusing because this 19 also includes the 10 that are taking Math as well.
Therefore:  students taking English and Social Studies ONLY.
3. Solve for c:
Similarly, we are given that 28 students are taking English and Math Therefore:  students taking English and Math ONLY.
4. Now we can solve for d, students who take English only:
33 students take English only.
Question 2)
We are given that a total of 54 students take math class. These students can be divided into 4 groups:
a = Students who take Math, English and Social Studies
c = Students who take Math and English only
e = Students who take Math and Social Studies only
f = Students who take Math only
a + c + e + f = 54 = Total students taking Math
Notice from question 1) we already have values for a and c so let's substitute:
 ,
so we don't have to do as much work for this part of the problem.
1. Solve for e:
The problem also tells us that 15 students take Math and Social Studies. This can be a little confusing because this 15 also includes the 10 that are taking English as well.
Therefore:  students taking Math and Social Studies ONLY.
2. Now we can solve for f, students who take Math only.
21 students take Math only.
Question 3)
We've already done the work for this one! The total number of students who take English and Social Studies only is 9. (Our b variable from question 1)
Question 4)
We've done this one too! The total number of students who take math and social studies only is 5 (Our e variable from Question 2)
Question 5)
In order to find how many students are not taking classes we need to find the total number students who ARE.
We have all the elements we need except for one:
a = students take all three classes = 10
b = students taking English and Social Studies DISABLED_event_only= 9
c = students taking English and Math DISABLED_event_only= 18
d = students taking English DISABLED_event_only= 33
e = students taking Math and Social Studies DISABLED_event_only= 5
f = students taking Math DISABLED_event_only= 21
g = students taking Social Studies DISABLED_event_only= ???
1. We need to find a value for g:
We are told that a total of 45 are taking Social studies. This includes:
a = 10 = students taking all three classes
b = 9 = students taking Social Studies and English only
e = 5 = students taking Social studies and Math only
g = ?
2. Solve for g:
21 students take Social Studies only
3. Subtract from total student body of 200:
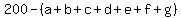 = Students not taking a class
 =
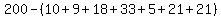83 students do not take English, Math or Social Studies.
Just a Reminder:
A Venn diagram would have made this problem a lot easier. You would simply draw 3 overlapping circles. Label one "Math", one "English" and one "Social Studies". Each section created by an overlap is equal to one of the letters we used (there should be 7, a through g). To keep track of the total number of groups of students simply count the number of sections and label each with a letter.
a) Sections where no overlap occurs are for those students enrolled in one class only (there will be three sections like this)
b) Sections where two of the circles overlap are for those students who are enrolled in two classes (there will be three of these)
c) There will be one section where all three circles overlap for the 10 students taking all three classes.
In math, it is always easier to have a picture of your problem handy!
|
|
|
| |
