Question 1208160: 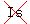 If x^2 + 5x + 7 is prime, show the  proof.
Found 4 solutions by Plocharczyk, Edwin McCravy, ikleyn, mccravyedwin:
Answer by Plocharczyk(17)   (Show Source):
You can put this solution on YOUR website!
x2 + 5x + 7
In order to determine whether the quadratic is prime or not, we need to decide
if it can be factorized. Any quadratic is prime if it cannot be factorized. The
quadratic in this example, x2 + 5x + 7, has a leading coefficient, or
coefficient of x2, equal to 1.
This means that it is a case of simple factorization, where we need to find two
numbers with a product of +7 and a sum of +5. The sum of the two numbers needs
to be the coefficient of x. And the product of the two numbers needs to be equal
to the free term. The only product of two integers that equals 7 is 1 and 7, as
1 multiplied by 7 is equal to 7.
However, these numbers do not have a sum of 5, as 1 plus 7 is equal to 8, not 5.
As there is no pair of numbers with a product of +7 and a sum of +5, we can say
that the quadratic x2 + 5x + 7 is prime and therefore cannot be factorized.
Edwin
Answer by Edwin McCravy(20056)  (Show Source):
Answer by ikleyn(52793)  (Show Source):
You can put this solution on YOUR website! .
The correct formulation of the problem is
Prove that x^2 + 5x + 7 is a prime polynomial.
The  meaning of this assignment is to prove that this given polynomial is a prime
over real coefficients polynomials. Again: not over the set of polynomial with integer coefficients,
but over much wider set of polynomials with real coefficients.
If x^2 + 5x + 7 is not a prime over the set of polynomials with real coefficients,
then it is a product of two linear binomials
x^2 + 5x + 7 = (ax+b)*(cx+d),
where a, b, c and d are real numbers. Since ab must be equal to 1, the coefficients "a" and "b"
must be non-zero real numbers. But then the polynomial x^2 + 5x + 7 has two real roots
 =  and  =  .
But, from the other hand, the discriminant of this quadratic polynomial is
" b^2 - 4ac " = 5^2 - 4*1*7 = 25 - 28 = -3,
which is negative number.
A quadratic polynomial with negative discriminant can not have real roots.
This contradiction proves that given polynomial x^2 + 5x + 7 is a prime in the set of
polynomial with real coefficients.
At this point, the proof is completed and the problem is solved in full.
You should clearly understand what is the difference in the formulation of the problem
and in its solution between my post and the post by Edwin.
This difference is a huge.
/////////////////////////
From this solution, one can formulate this simple criterion for a quadratic polynomial
with real coefficients to be a prime. The necessary and sufficient condition for it
is that this quadratic polynomial has negative discriminant.
/////////////////////
In response to Edwin's comment.
Edwin, I think that average middle school student don't know these words " prime polynomial "
and do not understand at all, what these words really mean, unless this student has an additional training
from outside, like a Math school, or a Math circle, or a personal Math teacher/trainer.
Therefore, I think that my solution is adequate and adequately targeted.
After your comment, Edwin, I searched Internet for key words " proving that a polynomial is prime ",
and first link from Google was THIS
https://virtualnerd.com/algebra-2/polynomials/equations/factoring-strategies/prime-polynomial-definition
which is, OBVIOUSLY, at least Algebra-II level.
For us, adult persons of the age 60 - 70 - 80, graduated in Math from universities in 60-ies and 70-ies,
these notions/conceptions " factoring polynomials " and " prime polynomials " look like very close.
But for young students, these notions/conceptions are separated by 3-5 years distance, at least.
In order to understand, what is a " prime polynomial ", a student should know/absorb
the notions " a field " and " a ring " from abstract Algebra, which is the level
of introductory undergraduate Math courses of college and/or university, in reality.
Edwin, I also looked into the reference in your post.
To me, it is bad style of teaching (anti-pedagogic), when the question asks about a notion/conception,
(a prime polynomial), which was not defined and explained previously.
If this author wants to be in good style and proposes this problem to 6-th grade students,
he/she must ask about factoring, not about "a prime polynomial".
And one more, probably, the last my note.
Edwin, why do you refer to other posts in the Internet to disprove my solution?
Do you think that they are more authoritative than my posts ?
It even does not come to my mind.
On the contrary, it seems to me that each my post should be carved
in stone and installed near each school for students and teachers to learn.
And in the dark hours of the day they should be additionally illuminated for better visibility.
Answer by mccravyedwin(407)  (Show Source):
You can put this solution on YOUR website!
It is obvious that this is a middle school student, Ikleyn, not a junior in
college. No junior in college is going to post a simple quadratic like
x^2 + 5x + 7.
I googled "proving that a polynomial is prime", and that told me that this is
an introductory middle school student in beginning factoring. Link to this video
will reveal what they're doing these days in middle school.
https://www.nagwa.com/en/videos/608139257981/#:~:text=In%20order%20to%20determine%20whether,%F0%9D%91%A5%20squared%20equal%20to%20one.
Go there are watch the video for kids in middle school. It is verbatim with
what I posted above only with a different simple quadratic.
Ikleyn over-judged the maturity of this student. If the student were an
advanced student, the question would be concerning prime and factorizable
general polynomials over rings, not a simple monic quadratic.
Edwin
|
|
|
