Question 1206953: The phone company, Splint, has a monthly cellular plan where the customer pays a flat monthly fee and then a cost of money per minute used on the phone. If the customer uses 360 minutes, the monthly cost is $126.00. If the customer uses 630 minutes, the monthly cost is $193.50.
Find a linear model of the form
where
is the number of monthly minutes used, and
is the total monthly cost of the Splint plan.
Using the equation from part a., find the total monthly cost if 883 minutes are used.
If 883 minutes are used, the total cost will be
dollars.
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The phone company, Splint, has a monthly cellular plan where the customer pays a flat monthly fee
and then a cost of money per minute used on the phone. If the customer uses 360 minutes,
the monthly cost is $126.00. If the customer uses 630 minutes, the monthly cost is $193.50.
Find a linear model of the form
where
is the number of monthly minutes used, and
is the total monthly cost of the Splint plan.
Using the equation from part a., find the total monthly cost if 883 minutes are used.
If 883 minutes are used, the total cost will be
dollars.
~~~~~~~~~~~~~~~~~~~~~~
From the problem, the difference 193.50-126.00 = 67.50 dollars corresponds to
630-360 = 270 minutes of the phone call.
So, 1 minute of the fall call costs 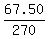 = 0.25 of a dollar.
Then the flat monthly fee is 126.00-0.25*360 = 36 dollars.
Thus the linear model is C(t) = 36.00 + 0.25t, where C(t)is the monthly fee,
t is the monthly minutes.
If 883 minutes is used, then the monthly fee is C(883) = 36.00 + 0.25*833 = 244.25 dollars. = 0.25 of a dollar.
Then the flat monthly fee is 126.00-0.25*360 = 36 dollars.
Thus the linear model is C(t) = 36.00 + 0.25t, where C(t)is the monthly fee,
t is the monthly minutes.
If 883 minutes is used, then the monthly fee is C(883) = 36.00 + 0.25*833 = 244.25 dollars.
Solved.
|
|
|