Question 1065804: As a rower passes under a bridge, a bottle of whiskey falls into the water.
Since it's half-full, it floats.
The rower doesn't hear it, and continues downstream.
After 20 minutes, he gets thirsty and looks for the bottle.
Having sobered some, he figures out that it fell into the water.
He turns around and rows upstream.
He finds the bottle 1 mile from the bridge.
***************
Find the speed of the current.
Found 4 solutions by Edwin McCravy, Alan3354, ikleyn, MathTherapy:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Suppose the man in the boat in the beginning is traveling south,
and when he turns around and comes back he travels north.
What I'm about to tell you to imagine is really weird, but you
can imagine it if you try.
Pretend that the river is still and the bank and bridge are
moving. [Yes, I said it was weird!} The man at first moves
south and the bridge moves north.
Then the bottle stays put and the bridge moves 1 mile north from
the bottle for 40 minutes, while the man goes south for 20 minutes
and back north to the bottle for another 20 minutes.
[Remember the bottle has not moved at all in the way we are imagining].
So the bridge has moved 1 mile from the bottle in 40 minutes, That's
the same as moving 3 miles in 120 minutes or 1.5 miles in 60 minutes
or 1.5 miles per hour.
The imagined speed of the bridge is the same as the speed of the
current.
Answer 1.5 mph.
Edwin
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A different perspective:
---
The boat and the bottle are in the same medium, the river, so they would stay together if not for the man rowing.
----
Instead of a bridge, envision this happening in open water near a marker, such as a buoy. The bottle stays near the marker.
The man rows 20 minutes away, so it takes him 20 minutes to row back, 40 minutes total.
-----
The bottle in the river moves 1 mile in 40 minutes --> 1.5 mi/hr.
==============
Choosing a frame of reference and remembering that "all motion is relative" makes it a simple problem.
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
When I read this problem condition yesterday morning, automatic switcher worked in my mind/(undermind), and another/different
version came to my conscionsness:
A rower goes upstream on a river. When passing under a bridge, a bottle of whiskey falls into the water.
Since it's half-full, it floats. The rower doesn't notice it, and continues going upstream.
After 20 minutes, he gets thirsty and looks for the bottle. Having sobered some, he figures out that it fell into the water.
He turns around and rows downstream. He finds the bottle 1 mile from the bridge. Find the speed of the current.
Yesterday in the evening I got understanding that I actually solved DIFFERENT problem than the original.
But thinking about the subject, I then got understanding that this SECOND formulation is actually BETTER than the original,
and is much more NATURAL.
Why ?? - If you read attentively both formulations, you will get "why".
The second formulation, which came from "my undermind" is much more natural from the point of view of human motivation than the original.
Indeed, WHO with the healthy mind will start rowing against the current to get the bottle ??
Much simpler is to stay "in place" and to wait when the current will bring/deliver the bottle.
So, now I think (and I am 120% sure) that my undermined formulation is much better, is much more realistic and is much more similar/closer
to the classic, than that what came first.
So, my solution below and everything what follows relates to the UPDATED formulation, and NOT TO THE ORIGINAL ONE.
Sorry that this new understanding came with a delay. But later is better than no-when.
I checked my sources, and now my statement is:
My changed formulation IS CLASSICAL.
That which came originally, IS NOT.
|
/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\
This problem is classic Travel and Distance problem. (with the corrections above !!)
Edwin provided its classic solution.
But his solution requires a powerful imagination.
For those who experiences a lack of such imagination (as myself), I will give another solution.
Let "u" be the rower speed in "still water" and "v" be the current speed (in miles per hour).
From that moment, when the rower figured out that the bottle fell into water,
from the same moment when he turned around and start catching the bottle, we have a classic "catching up" problem.
Namely, we have the rower at the distance of 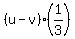 upstream the bridge, and we have a bottle at the distance upstream the bridge, and we have a bottle at the distance 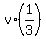 downstream the bridge.
What is downstream the bridge.
What is  here ? - But of course, it is here ? - But of course, it is  of an hour, or 20 minutes.
At this moment we turn ON our chronometer, we start counting the time, and what we see ? What do we observe ?
Starting from this moment and till the moment "t" of catching up the bottle, the rower will cover the distance
D = (the distance back to the bridge) + (the distance the bottle went downstream in of an hour, or 20 minutes.
At this moment we turn ON our chronometer, we start counting the time, and what we see ? What do we observe ?
Starting from this moment and till the moment "t" of catching up the bottle, the rower will cover the distance
D = (the distance back to the bridge) + (the distance the bottle went downstream in  of an hour) + (the distance bottle went downstream during the time "t") = of an hour) + (the distance bottle went downstream during the time "t") =
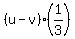 + + 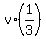 + + 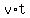 =
= =
=  + + 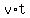 = = 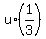 + + 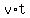 .
Calculating this distance by another way (using the speed (u+v) of the rower downstream) we can express this distance as
D = .
Calculating this distance by another way (using the speed (u+v) of the rower downstream) we can express this distance as
D = 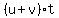 .
The distance is the same (!!!), so we have an equation .
The distance is the same (!!!), so we have an equation
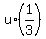 + + 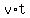 = = 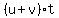 .
Simplify it in one more step, and you get A REMARKABLE EQUALITY:
t = .
Simplify it in one more step, and you get A REMARKABLE EQUALITY:
t =  .
Which means (and we PROVED it) that the catching time is exactly .
Which means (and we PROVED it) that the catching time is exactly  of an hour.
The thing which was not obvious from the beginning !
Now we are at the finish line. One step to the end. To the VICTORY !!
We have another condition: for 20 minutes plus "t" minutes the bottle traveled exactly one mile !
It means that of an hour.
The thing which was not obvious from the beginning !
Now we are at the finish line. One step to the end. To the VICTORY !!
We have another condition: for 20 minutes plus "t" minutes the bottle traveled exactly one mile !
It means that 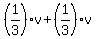 = 1, or = 1, or 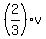 = 1, or (AT LAST !!!) v = = 1, or (AT LAST !!!) v =  miles per hour. miles per hour.
SOLVED. SOLVED. SOLVED.
---------------------
I am a mathematician by my basic education, so my mind works automatically in attempting to reverse / to transform the nonsense to
some sensible. So it was in this case (as in many other cases).
''''''''''''''''''''''''''''
Now I have a question to the person who posted (or invented ?) the original post:
Why (or for what reason) do you distribute this original the half-false formulation of the beautiful problem
carefully designed hundreds years ago by those who really know and love MATH ???
The problems like this one (corrected by me) are/is a treasure, literally.
And they require an adequate treatment, too.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
As a rower passes under a bridge, a bottle of whiskey falls into the water.
Since it's half-full, it floats.
The rower doesn't hear it, and continues downstream.
After 20 minutes, he gets thirsty and looks for the bottle.
Having sobered some, he figures out that it fell into the water.
He turns around and rows upstream.
He finds the bottle 1 mile from the bridge.
***************
Find the speed of the current.
I found this problem quite interesting, and so decided to solve it.
Let speed of boat in still water, and speed of current, be S, and C, respectively
Then average speed going DOWNSTREAM, and UPSTREAM are: S + C, and S C, respectively
Time bottle (and rower) took to get to MEETUP point = 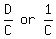
Distance hed traveled before noticing the missing bottle: 
Distance he traveled to get back to bottle: 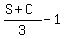
Also, distance he traveled to get back to bottle: 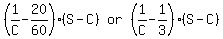
We then get: 

 -------- Multiplying by LCD, 3C -------- Multiplying by LCD, 3C


2CS 3S = 0
S(2C 3) = S(0)
2C 3 = 0
2C = 3
C, or speed of current = 
|
|
|