Question 1027853: Five different positive integers added two at a time give the
following sums: 16, 20, 22, 23, 25, 28, 29, 30, 34, and 37. Find
the product of the five integers.
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Five different positive integers added two at a time give the following sums: 16, 20, 22, 23, 25, 28, 29, 30, 34, and 37.
Find the product of the five integers.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I agree with Mr. Edwin McCravy that my solution was wrong.
Mr. Edwin McCravy, thank you for your critics and detecting the error.
I still keep my old solution below for documentary purposes (but probably will delete it later).
Instead, I will put here the other solution, which is shorter.
Let the numbers be a < b < c < d < e
Then the smallest two, a and b, must have sum 16,
a + b = 16
and the largest two, d and e, must have sum 37,
d + e = 37.
----------------------------------------------------------------------
Previous 5 lines are exactly from Mr. McCravy solution, but what follows is different.
----------------------------------------------------------------------
Then the middle number c is equal to 66 - (a+b) - (d+e) = 66 - 16 - 37 = 13.
(The number 66 goes from my old solution which is correct to this point).
OK. So, the two smallest numbers a and b give the sum of 16, and the third number is 13.
It means that the next sum, 20 (see the condition) is a+c.
It can not be nothing else.
If a + c = 20 and c = 13, then a = 20 - 13 = 7.
It implies b = 16-7 = 9.
So, the first three numbers are a = 7, b = 9 and c = 13.
OK. Now we can make the similar analysis from the other end.
So, the two largest numbers d and e give the sum of 37, and the third number in the descending order is 13.
It means that the next from the largest sum, 34 (see the condition) is e+c.
It can not be nothing else.
If e + c = 34 and c = 13, then e = 34 - 13 = 21.
It implies d = 37-21 = 16.
Thus the numbers are 7, 9, 13, 16 and 21.
Their product is 275184.
Below is my old >>>wrong<<< solution.
It is still valid in the part that the sum of the five numbers is 66.
What follows after that is wrong.
Let  , ,  , ,  , ,  and and  be our five different positive integers.
We are given that be our five different positive integers.
We are given that
 + +  = 16, (1) = 16, (1)
 + +  = 20, (2) = 20, (2)
 + +  = 22, (3) = 22, (3)
 + +  = 23, (4) = 23, (4)
 + +  = 25, (5) = 25, (5)
 + +  = 28, (6) = 28, (6)
 + +  = 29, (7) = 29, (7)
 + +  = 30, (8) = 30, (8)
 + +  = 34, (9) = 34, (9)
 + +  = 37. (10)
Add all ten equations (1) - (10) at once (both left and right sides). You will get an equation = 37. (10)
Add all ten equations (1) - (10) at once (both left and right sides). You will get an equation
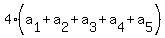 = = 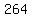 , or, after dividing both sides by 4 , or, after dividing both sides by 4
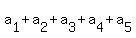 = = 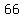 . (*)
Now distract, one by one and one after one, the above equations (10), (9), (8), (7) and (3) from the equation (*) as it is shown below. . (*)
Now distract, one by one and one after one, the above equations (10), (9), (8), (7) and (3) from the equation (*) as it is shown below.
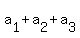 = 29, (11) ( distract (10) from (*); 29 = 66 - 37 ) = 29, (11) ( distract (10) from (*); 29 = 66 - 37 )
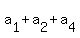 = 32, (12) ( distract (9) from (*); 32 = 66 - 34 ) = 32, (12) ( distract (9) from (*); 32 = 66 - 34 )
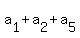 = 36, (13) ( distract (8) from (*); 36 = 66 - 30 ) = 36, (13) ( distract (8) from (*); 36 = 66 - 30 )
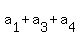 = 37, (14) ( distract (7) from (*); 37 = 66 - 29 ) = 37, (14) ( distract (7) from (*); 37 = 66 - 29 )
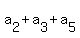 = 44, (15) ( distract (3) from (*); 44 = 66 - 22 )
Now, compare (1) and (11). You will get = 44, (15) ( distract (3) from (*); 44 = 66 - 22 )
Now, compare (1) and (11). You will get  = 29 - 16 = 13. (16)
Next, compare (1) and (12). You will get = 29 - 16 = 13. (16)
Next, compare (1) and (12). You will get  = 32 - 16 = 16. (17)
Compare (1) and (13). You will get = 32 - 16 = 16. (17)
Compare (1) and (13). You will get  = 36 - 16 = 20. (18)
Compare (8) and (14). You will get = 36 - 16 = 20. (18)
Compare (8) and (14). You will get  = 37 - 30 = 7. (19)
Compare (9) and (15). You will get = 37 - 30 = 7. (19)
Compare (9) and (15). You will get  = 44 - 34 = 10. (20)
Now, to answer the question, multiply the right sides of (16) - (20). You will get = 44 - 34 = 10. (20)
Now, to answer the question, multiply the right sides of (16) - (20). You will get
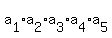 = 13*16*20*7*10 = 291200.
Answer. The product of five numbers is 291200. = 13*16*20*7*10 = 291200.
Answer. The product of five numbers is 291200.
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We let the numbers be a < b < c < d < e
Then the smallest two, a and b, must have sum 16,
a + b = 16
and the largest two, d and e, must have sum 37,
d + e = 37.
[Those are the only two pairs that we can be sure
have the smallest and largest sums. We can't be
sure about the other pairs.]
If the smallest number, a, is too small we won't
be able to get all those large sums. So let's
take the smallest, a, to be as large as possible
We'll begin by trying a=7 and b=9, so that 7+9=16.
We need to be able to get 20 by adding two numbers,
so we need to add 13 to the 7 to get the 20. [Note
that we'd have to add 4 to the 9, and 4 is too small.]
We take c=13, so that 7+13=20.
We can now also get 22, since 9+13=22.
We have so far, a=7, b=9, c=13.
So d is larger than 13.
d can't be 14 because 14+13=27 which is not one of
the sums.
d can't be 15 because 15+9=24 which is not one of
the sums.
But d can be 16, because 7+16=23, which is one of
the sums.
Also 9+16=25, which is one of the sums.
We have so far, a=7, b=9, c=13, d=16
Now since d + e = 37, e can only be 21,
so that 16+21=37
Answer: a=7, b=9, c=13, d=16, e=21
Checking:
7+ 9 = 16
7+13 = 20
9+13 = 22
7+16 = 23
9+16 = 25
7+21 = 28
13+16 = 29
9+21 = 30
13+21 = 34
16+21 = 37
The product is 7*9*13*16*21 = 275184
Edwin
|
|
|