Question 1017725: An original number is increased by k%, and then the result is decreased by w%. The final result is 85% of the original number. If k is a positive integer less than 173 and if w is a positive integer, find the sum of all possible distinct values of k.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = the original number = the original number
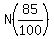 = 85% of the original number = 85% of the original number
 = the original number increased by = the original number increased by  . .
Increasing a number by  is multiplying it by is multiplying it by 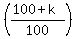 . .
Similarly, decreasing a number  by by 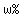 is multiplying it by is multiplying it by 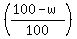 : :
 . .
So,
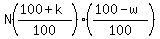 = the original number first increased by = the original number first increased by  , and then decreased by , and then decreased by 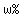 . .
Our equation is





Now we need pairs of factors of 
There should be  factors, which come in factors, which come in  pairs: pairs:
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , and , and
 . .
Since 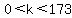 , , 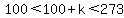 . .
The only factors that could be 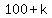 are are  , ,  , and , and 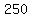 . .
 ---> ---> ---> ---> , or , or
 ---> ---> ---> ---> , or , or
 ---> ---> ---> ---> . .
|
|
|