Questions on Algebra: Expressions involving variables, substitution answered by real tutors!

Tutors Answer Your Questions about Expressions-with-variables (FREE)

Question 1180164: -x + 3y = 2 and x - 5y = -4 Solving for Two Variables using Elimination
Click here to see answer by ikleyn(53570)

Question 44251: can someone please help me with this problem: 1/3x+6 +2 = 3/x+2
Click here to see answer by MathTherapy(10702)

Question 1210515: in a certain freshman class the number of girls is 83 less than twice the number of boys(b) the total number of students in that freshman class is 259 how many girls and boys are in that class
Click here to see answer by josgarithmetic(39720)

Question 456599: How do I substitute a problem like this?
y = x + 3
y = 2x + 12
Click here to see answer by timofer(139)

Question 456599: How do I substitute a problem like this?
y = x + 3
y = 2x + 12
Click here to see answer by ikleyn(53570)

Question 454327: Solve the linear system by using substitution. 3x+2y=5, 5x-9y=-4
Click here to see answer by josgarithmetic(39720)

Question 454327: Solve the linear system by using substitution. 3x+2y=5, 5x-9y=-4
Click here to see answer by ikleyn(53570)

Question 451898: How do I set this problem up:
If a farmer stand owner mixes apple juice and cranberry juice, how much should he charge if he mixes 8L of apple juice selling for 45 cents a liter with 10L of cranberrt juice sellling for $1.08 a liter.
Click here to see answer by ikleyn(53570)

Question 449484: Solve by the elimination method.
0.3x-0.2y=4
0.2x+0.5y=-75/17
Click here to see answer by ikleyn(53570)

Question 447774: how to simplify sqrt (12ab^3c^2)
Click here to see answer by ikleyn(53570)

Question 445209: i'm trying to show a=b or a=1/b without plugging in the values for a.
this is the equation
a+1/a=b+1/b
i have tried multiplying both sides by ab
i tried the quadratic equation but that didn't work very well cause i couldn't get the square root out
i just need a step by step explanation of how to get there cause its driving me crazy and i think i'm just missing something simple
please remember. i know how to substitute. i'm basically proving a= b,1/b
which is why i tried making it a quadratic because i knew there were 2 answers
thank you very much
i hope you can help
Click here to see answer by ikleyn(53570)

Question 444146: 6x - y = 39
6x + 7y=33
Click here to see answer by josgarithmetic(39720)

Question 444146: 6x - y = 39
6x + 7y=33
Click here to see answer by ikleyn(53570)

Question 436132: Word problem.
It takes 60 minutes to fill a pond with water alone.
It takes 80 minutes to drain a pond of water alone.
How long will it take to fill the pond while it is being drained at the same time?
Click here to see answer by josgarithmetic(39720)

Question 421830: -4x-2y=-8 y=-2x+4
Click here to see answer by ikleyn(53570)

Question 730274: A company manufactures an alarm clock. Three weeks ago the had 250 on hand. Two weeks from now it will have 500. Assume the company will continue to make the clocks at this same rate

Click here to see answer by ikleyn(53570)

Question 733492: how would i solve this equation : (2t)^4*3^3
Click here to see answer by josgarithmetic(39720)

Question 733492: how would i solve this equation : (2t)^4*3^3
Click here to see answer by ikleyn(53570)

Question 737462: The width of a rectangle is 18 feet less than the perimeter. the area of the rectangle is 2,040 square feet. What are the dimensions of the rectangle?
Click here to see answer by ikleyn(53570)

Question 612274: I have two algebra I word problems i need help setting up. I would like if you can explain the steps of setting up.
Here it is:
Problem #1
The length of a rectangle is 2 1/2 times its width. Its area is 90 square units. What are its dimensions? (Hint: length times width = area)
Let w= width in units.
L=(2 1/2)w= 5w/2 = length in units

Click here to see answer by MathTherapy(10702)

Question 747745: Some of Aaron's friends are planning to buy him a gift worth 270, dividing the cost equally among themselves. Six more of his friends decided to share in the expenses and so each one's share is decreased by 12. How many friends were originally part of the plan?
Click here to see answer by ikleyn(53570)

Question 869743: The sum of 4 times a number and 2 is 18. What is the number?
Click here to see answer by timofer(139)

Question 479860: I am working on my math packet for school. I came across a section in it, in which i completely forgot how to do. i asked my family and they helped me on most of the problems but they couldn't help me figure this one out.
I am suppose to determine the answer for each problem. Simplify when possible:
Here is the equation: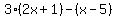
I've tried combining the "x"s and I have also tried using the order of operations but no matter what i use, it seems like i can't solve it.
If you could go through each step and explain what you did and why you did it, i would make it much easier for me to understand and i would greatly appreciate it.

Click here to see answer by ikleyn(53570)

Question 500890: please help me with this question.
Express in terms of odd and even numbers why the number 286 would not appear in the series 4, 12, 24, 40... ?

Click here to see answer by ikleyn(53570)

Question 553434: solve the system of equations using the substitution method
x+z=8
y-z=5
x-y=9
Click here to see answer by MathTherapy(10702)

Question 553434: solve the system of equations using the substitution method
x+z=8
y-z=5
x-y=9
Click here to see answer by ikleyn(53570)

Question 1160143: How would I write the following so the coefficient is in front?
1. (3y)8
2. 3(4b)
Click here to see answer by ikleyn(53570)

Question 1209923: Let x, y, and z be real numbers. If x^2 + y^2 + z^2 = 1, then find the maximum value of
3x + 4y + 5z + x^3 + \frac{4x^2*y)/{z} + \frac{z^5}{xy^2}
Click here to see answer by ikleyn(53570)

Question 1210272: (-9x + 57)^x = 729,
find x.
Click here to see answer by Edwin McCravy(20077)

Question 1209973: Let a and b be positive real numbers. Let
m = \min \left\{ a, \frac{1}{b}, b^2 + \frac{1}{a + 1} \right\}.
Find the largest possible value of m.

Click here to see answer by mccravyedwin(419)

Question 1209926: (a) Let x, y, and z be positive real numbers. Find the largest possible value of
\sqrt{\frac{3x + 5y + 2z}{6x + 5y + 4z}} + \sqrt{\frac{2x + 5y + z}{6x + 5y + 5z}} + \sqrt{\frac{9x + y + 4z}{6x + 5y + 4z}}.

(b) Find \frac{z}{x} if (x,y,z) is a triple that gives the maximum value in Part (a).

Click here to see answer by mccravyedwin(419)

Question 1209935: Let a, b, and c be positive real numbers. If a + b + c = 1, then find the minimum value of
\frac{1}{a} + \frac{1}{b} + \frac{1}{c*a^2} + \frac{2}{ab^2} + \frac{8}{c^3}.
Click here to see answer by CPhill(2189)

Question 1209936: Let a, b, and c be positive real numbers. If a + b + c = 1, then find the minimum value of
\frac{1}{a} + \frac{1}{b} + \frac{4}{c*a^2} + \frac{16}{b^4*a} + \frac{32}{a*b^3}
Click here to see answer by CPhill(2189)

Question 1209927: The real numbers x_1, x_2, x_3, x_4, and x_5 satisfy
x_1 + x_2 + x_3 + x_4 + x_5 = 8,
x_1^2 + x_2^2 + x_3^2 + x_4^2 + x_5^2 = 12,
x_1^3 + x_2^3 + x_3^3 + x_4^3 + x_5^3 = 16.

Let m be the smallest possible value of x_5, and let M be the largest possible value of x_5. Enter the ordered pair (m,M).

Click here to see answer by CPhill(2189)

Question 1209925: Let x_1, x_2, \dots, x_{100} be real numbers. If
x_1^2 + 2x_2^2 + \dots + 100x_{100}^2 = 1,
then find the maximum value of x_1/1 + x_2/2 + \dots + x_{100}/100.
Click here to see answer by CPhill(2189)

Question 1209918: Let x_1, x_2, \dots, x_n be real numbers. If
x_1 + 2x_2 + \dots + nx_n = 1,
then find the minimum value of x_1^2/1 + x_2^2/2 + \dots + x_n^2/n, in terms of n.

Click here to see answer by CPhill(2189)

Question 1209919: Let x_1, x_2, \dots, x_n be real numbers. If
x_1^2 + 2x_2^2 + \dots + nx_n^2 = 1,
then find the maximum value of (x_1 + x_2/2 + \dots + x_n/n)^2, in terms of n.
Click here to see answer by CPhill(2189)

Question 1209917: Let a, b, and c be positive real numbers. Find the minimum value of
(a + 1)^2 + \left( \frac{b}{a} + a + 1 \right)^2 + \left( \frac{c}{b} + abc \right)^2 + \left( \frac{4}{c} + \frac{c}{a} \right)^2.
Click here to see answer by CPhill(2189)

Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790, 11791..11835, 11836..11880, 11881..11925, 11926..11970, 11971..12015, 12016..12060, 12061..12105, 12106..12150, 12151..12195, 12196..12240, 12241..12285, 12286..12330, 12331..12375, 12376..12420, 12421..12465, 12466..12510, 12511..12555, 12556..12600, 12601..12645, 12646..12690, 12691..12735, 12736..12780, 12781..12825, 12826..12870, 12871..12915, 12916..12960, 12961..13005, 13006..13050, 13051..13095, 13096..13140, 13141..13185, 13186..13230, 13231..13275, 13276..13320, 13321..13365, 13366..13410, 13411..13455, 13456..13500, 13501..13545, 13546..13590, 13591..13635, 13636..13680, 13681..13725, 13726..13770, 13771..13815, 13816..13860, 13861..13905, 13906..13950, 13951..13995, 13996..14040, 14041..14085, 14086..14130, 14131..14175, 14176..14220, 14221..14265, 14266..14310, 14311..14355, 14356..14400, 14401..14445, 14446..14490, 14491..14535, 14536..14580, 14581..14625, 14626..14670, 14671..14715, 14716..14760, 14761..14805, 14806..14850, 14851..14895, 14896..14940, 14941..14985, 14986..15030, 15031..15075, 15076..15120, 15121..15165, 15166..15210, 15211..15255, 15256..15300, 15301..15345, 15346..15390