Question 794840: Determine all integers n such that n^4-4n^3+15n^2-30n+27 is a prime number
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 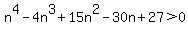 for all real values of for all real values of  , ,
so there are no factors of the form 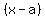 , ,
but I can still factor that polynomial into the product of two quadratic polynomials:

Multiplying, I get

I need to find b, c, d, and e such that
 , so the set , so the set 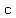 is {1,27}, or {-1,-27}, or {3,9}, or {-3,-9} is {1,27}, or {-1,-27}, or {3,9}, or {-3,-9}

 and and

Since c and e are both odd, 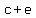 will be even, will be even,
and  must be odd to make must be odd to make 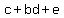 odd, let alone odd, let alone 
To make  odd, b and d must both be odd. odd, b and d must both be odd.
They have to add up to  too to make too to make 
There are many options, but With the set {b,d}={-1,-3} I could get
 and and
 , which with {c,e}={3,9}, , which with {c,e}={3,9},
added to  to make to make 
Trying the options left for the order of the numbers in each set,
 could be made pairing them as could be made pairing them as 
with  , ,  , ,  , and , and  . .
So 
With  being an integer, the factors being an integer, the factors
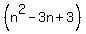 and and 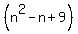 are integers. are integers.
For their product to be a prime number, one factor must be 1,
and the other factor must be a prime number.
Making the first factor equal to 1, we get
 --> --> --> --> --> --> --> -->
 --> --> leads us to leads us to
the solution  , ,
which makes 
 also makes also makes  , but it makes , but it makes
 and 9 is not a prime number. and 9 is not a prime number.
Making the second factor equal to 1, we get
 --> --> --> --> , which has no real solutions. , which has no real solutions.
NOTE: When you find a problem that seems to difficult for mere humans, like us, try the artofproblemsolving community forum. The members there can't resist a challenge, and if it proves too difficult for the level where you post it, the moderators may bump it up. Start where you think is to low (try high school intermediate or lower) so you do not offend them by posting problems that are insultingly easy for them. I bet some 12 or 13-year old will show you how easy your problem is.
|
|
|