Question 477751: what is the unit digit of 7raisedto 155 how to solve it?
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! there will be a patten to the units digit.
7^0 = 1 last digit = 1
7^1 = 7 last digit = 7
7^2 = 49 last digit = 9
7^3 = 343 last digit = 3
7^4 = 2401 last digit = 1 ***** (pattern starts to repeat itself here)
7^5 = 16807 last digit = 7
7^6 = 117649 last digit = 9
7^7 = 8234543 last digit = 3
7^8 = 5764801 last digit = 1 ***** (pattern repeats again here)
7^9 = 40353607 last digit = 7
7^10 = 282475249 last digit = 9
7^11 = 1977326743 last digit = 3
7^12 = 13841287201 last digit = 1 ***** (pattern repeats again here)
the pattern repeats itself every 4 exponents.
make a rule from this and apply it to the larger exponent.
7^0 = 1
7^4 = 1
7^8 = 1
if you divide the exponent by 4, you will get the first digit in the sequence.
4/4 = 1.0 which means the last digit is 1
5/4 = 1.25 which means the last digit is 7
6/4 = 1.5 which means the last digit is 9
7/4 = 1.75 which means the last digit is 3
8/4 = 2.0 which means the last digit is 1
9/4 = 2.25 which means the last digit is 7
10/4 = 2.5 which means the last digit is 9
11/4 = 2.75 which means the last digit is 3
12/4 = 3.0 which means the last digit is 1
this is substantiated by the table above.
the rule can be developed as follows:
if the fractional part is 0, then the last digit is 1
if the fractional part is .25, then the last digit is 7
if the fractional part is .5, then the last digit is 9
if the fractional part is .75, then the last digit is 3
applying that rule to your problem, we get:
7^155 results in a last digit of:
155/4 = 38.75
the fractional part is .75 so the last digit is 3.
Answer by ikleyn(53426)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
What is the unit digit of 7 raised to 155 ? How to solve it?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The problems of this type are very popular.
You often can find them in tests, in Math competitions, in Math Olympiads, in entrance exams
and even in the interview.
Therefore, to be successful in all these aspects, you need to know VERY FIRMLY
HOW TO solve such problems.
If such a problem is given to you, the right solution should bounce off you
like a ball bounces off a wall.
- - - - - - - - S O L U T I O N - - - - - - - -
If you will rise your number 7 in consecutive degrees, you will find very soon, that the last
digit is repeating.
This is not accidental - it is natural.
Indeed, every time you rise to the next degree, the last digit is a result of multiplication
of the previous last digit by 7.
But the number of possible last digits is limited: it is only 10, because there are 10 digits,
from 0 to 9, in all.
Therefore inevitably, some last digit will repeat one of preceding last digits.
As soon as it will happen for the first time, the digits will be repeating cyclically.
Let's consider how it works in our case. I will not write whole many-digit numbers,
since there is no need in it. I only will write and track the last digit.
degree k 1 2 3 4 5 6 7 8 9
the last digit 7 9 3 1 7 9 3 1 7
of 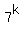 You see that first time repeating happens at k = 5, and after k=4 the cycle (7,9,3,1) is repeating again and again.
So, for
You see that first time repeating happens at k = 5, and after k=4 the cycle (7,9,3,1) is repeating again and again.
So, for 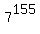 , there are many repeating cycles of the length 4 - they are not interesting for us.
The number 155 gives the remainder 3 when divided by 4: 155 = 4*38 + 3.
It tells us that the sough last digit in the number , there are many repeating cycles of the length 4 - they are not interesting for us.
The number 155 gives the remainder 3 when divided by 4: 155 = 4*38 + 3.
It tells us that the sough last digit in the number 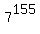 is the third term in the basic cycle of four digits {7, 9, 3, 1}.
From it, we conclude that the last digit of the number is the third term in the basic cycle of four digits {7, 9, 3, 1}.
From it, we conclude that the last digit of the number 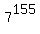 is 3, since '3' is the third term of the cycle {7, 9, 3, 1}. is 3, since '3' is the third term of the cycle {7, 9, 3, 1}.
Solved.
It is HOW TO such problems should be solved and analyzed.
|
|
|