Question 281835: Simplify. Explain the work please.
(3m^-1n^4)^-2(2m^3n^-5)^4
Answer by JenniferTutors(83)   (Show Source): (Show Source):
You can put this solution on YOUR website! For this equation:
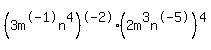
Follow the order of operations, work within the parenthesis first.
Now inside the parenthesis, you'll notice you have negative exponents, now you have to change that to the reciprocal to make it positive (put it on the denominator in this case):
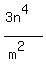 x x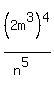
A lot has changed, I'll explain: In the first parenthesis, The 3 stayed on the numerator, it has no negative exponents, The m moved to the denominator because it had a negative 1 exponent, and the negative exponent 2 in the first parenthesis was carried to the bottom, which multiplied m to make it 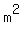 . .
The second parenthesis, the  and and  stayed on the numerator because there were no neg exponents. The stayed on the numerator because there were no neg exponents. The  moved to the denominator because it had a negative exponent. The positive exponent 4 stayed on the numerator (not a negative exponent), to look like this moved to the denominator because it had a negative exponent. The positive exponent 4 stayed on the numerator (not a negative exponent), to look like this 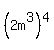
Now the next step:
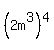 Distribute the 4 into the parenthesis Distribute the 4 into the parenthesis 
Distribute the 4 to the  & Multiply the exponents & Multiply the exponents 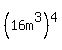 3 x 4 = 12. 3 x 4 = 12.
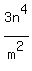 x x
Now, cross out like terms by subtracting, see here:
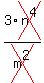 x x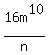
See, in the first parenthesis we crossed out the 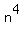 because there were 5 in the other equation, by subtracting like terms, that leaves 1 in the second parenthesis and none in the first. Also crossed out the m in the first parenthesis for the same reason, by subtracting like terms there were 12 m's in the second parenthesis, now by like terms there is only 10. because there were 5 in the other equation, by subtracting like terms, that leaves 1 in the second parenthesis and none in the first. Also crossed out the m in the first parenthesis for the same reason, by subtracting like terms there were 12 m's in the second parenthesis, now by like terms there is only 10.
Next step:
Multiply across
 x x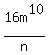
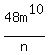
Hope that helps.
|
|
|