Question 1204752: If 6^(2x+1) = k, then 6^(4x+3) equals
A 12k
B k^2 + 6
C 6k^2
D 2k + 6
E 36k^2
Found 4 solutions by ikleyn, Edwin McCravy, math_tutor2020, MathTherapy:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
If 6^(2x+1) = k, then 6^(4x+3) equals
A 12k
B k^2 + 6
C 6k^2
D 2k + 6
E 36k^2
~~~~~~~~~~~~~~~~~~~~
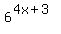 = trace/watch attentively each and every my step =
=  =  =  =  .
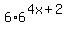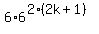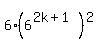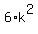ANSWER. Option (C).
Solved.
Is everything clear to you from my solution ?
--------------------
In this problem, we have a given basic equation 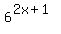 = k and an expression to evaluate .
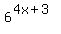An idea of the method is to transform the given "expression to evaluate" step by step to get the given basic expression
in it somewhere on the way, and then to replace one side of the given basic expression by its other side.
Then a miracle will happen literally in front of your eyes and you will get the required proof
(or evaluation, or reduction) in minutes ( ! )
If you will solve such problem once in your life (or if somebody will show you this trick
once in your life, as I do it here for you), you will MEMORIZE it and will be able to repeat it
in hundreds other similar problems/cases in your life.
It is worth to memorize HOW it works - then you will have a wonderful mathematical weapon in your possessions ( ! )
In his post, tutor @math_tutor2020 repeated my solution practically with no change - thanks to him for it,
even although he did not mention about it. Probably, he forgot to mention, or couldn't find the right/appropriate words.
---------------------
Dear tutor @math_tutor2020, when I tell about mentioning, I worry not about my rights.
I worry about a reader / (a student): what he will think by seeing
two identical texts in one post ? - At least, he will have mess in his/her mind.
It is what I'd like to avoid.
Answer by Edwin McCravy(20054)  (Show Source):
You can put this solution on YOUR website!
Here's what to do in an EMERGENCY, but only in an EMERGENCY,
and only on a multiple-choice test where you don't have to
show your work.
If you run into a problem like this on a multiple-choice
test and don't know what to do, and are completely stuck,
then here is a trick that works a lot of the time. Some other
tutors here will frown on me for telling you this, but it
works sometimes on certain problems.
Substitute x=0.
Then 6^(2*0+1) = 6 = k, then 6^(4*0+3) = 6^3 = 216
Then substitute 6 for k in every one of the choices:
A) 12k = 12(6) = 72
That's not 216, so that eliminates A
B) k^2 + 6 = (6)^2 + 6 = 42
That's not 216, so that eliminates B
C) 6k^2 = 6(6)^2 = 6(36) = 216
That IS 216, but that only means it's POSSIBLY the right choice.
For it happens sometimes that one of the others will also be 216.
D) 2k + 6 = 2(6) + 6 = 18.
That's not 216, so that eliminates D
E) 36k^2 = 36(6)^2 = 1296
That's not 216, so that eliminates E
So we know the correct choice is C.
If another one of them had also come out 216, then
you could do it again by substituting x=1 or x=-1.
But if you're short on time, you still have a better
chance of guessing correctly.
Also sometimes, on some problems, substituting 0 in what's
given and then in all the choices is the easiest method!
Sometimes you can do it in your head! I have actually used
it myself to save time even though I knew how to get the
solution the regular way!
As I mentioned above, sometimes substituting 1 or -1 is
better than 0. Sometimes substituting 0 causes a denominator
to be 0. Other times other numbers work better. So you can
improvise on this method. But I'd better warn you, you'd
better not rely on this method! It won't save you if you
don't understand the material!
Edwin
Answer by math_tutor2020(3816)  (Show Source):
You can put this solution on YOUR website!
Answer: Choice C) 6k^2
-------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------
Work Shown
Method 1
I reached this independently of ikleyn, so there's no citation needed.
---------------------------
Method 2
---------------------------
Method 3
Let 
Use graphing software like Desmos or GeoGebra to graph each of the five answer choices A through E as separate functions.
Some teachers will allow graphing tech like that during exams, so it depends on the teacher. Often the app is set to exam mode to be for limited cases. Meaning you won't have access to the CAS feature for instance.
Anyways, set up f(x) = 6^(2x+1) in the first box.
12k for instance would be 12*f(x), k^2+6 would be (f(x))^2 + 6, and so on.
There would be 6 functions defined so far.
As the seventh function, plot 6^(4x+3) to see what curve perfectly aligns to it.
It should be 6*( f(x) )^2
Here's an example comparing answer choice B to 6^(4x+3)
https://www.desmos.com/calculator/kivtpkjz6r
The curves do not overlap, so we can rule choice B out.
However, if we plot choice C and 6^(4x+3) together, then we get this perfect overlap
https://www.desmos.com/calculator/xbdq1rhx20
Click the round button for graph 7 to turn it off, then click it back on. Repeatedly do this to have the curve blink two different colors to show the overlap.
---------------------------
Method 4
We'll use graphing software similar to method 3.
Define f(x) = 6^(2x+1)
Then
A(x) = 12*f(x)
B(x) = (f(x))^2+6
C(x) = 6*(f(x))^2
D(x) = 2*f(x)+6
E(x) = 36*(f(x))^2
are the five answer choices, and we want to check against
G(x) = 6^(4x+3)
To see if two function curves are the same, we can subtract them and see which produces a horizontal flat line over the x axis.
Through trial-and-error, you should find that C(x) - G(x) will produce that flat line we're after.
It means C(x) - G(x) = 0 for all x in the domain, which leads to C(x) = G(x)
It's the same idea as saying something like 2+3 = 5, so 2+3-5 = 0.
---------------------------
Method 5
Use the route that tutor Edwin took.
It's a useful strategy for exams involving multiple choice (when in a time crunch and/or when completely stumped).
x = 0 is a common easy value to work with. It leads to 6^(4x+3) = 216 and k = 6.
You can then plug that k value into each answer choice to see which gives you 216.
If you had more than one answer choice produce 216, then pick something else for x.
Answer by MathTherapy(10551)  (Show Source):
|
|
|
