Question 1198080: Find the periodic payments PMT necessary to accumulate the given amount in an annuity account. (Assume end-of-period deposits and compounding at the same intervals as deposits. Round your answer to the nearest cent.)
$50,000 in a fund paying 5% per year, with monthly payments for 5 years, if the fund contains $10,000 at the start
Found 2 solutions by ElectricPavlov, ikleyn:
Answer by ElectricPavlov(122)   (Show Source): (Show Source):
You can put this solution on YOUR website! The periodic payment required to accumulate $50,000 in a fund paying 5% per year with monthly payments for 5 years, starting with an initial balance of $10,000, is approximately **$546.52**.
Answer by ikleyn(53426)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The periodic payments PMT necessary to accumulate the given amount in an annuity account.
(Assume end-of-period deposits and compounding at the same intervals as deposits).
$50,000 in a fund paying 5% per year, with monthly payments for 5 years, if the fund contains $10,000 at the start.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let solve the problem in 2 steps.
Step 1
The future value of the initial amount of $10,000 in 5 years will be
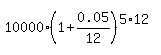 = = 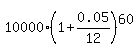 = 12,833.59 dollars.
Thus, making monthly deposits of X dollars, we should accrue the rest 50000 - 12833.59 = 37166.41 dollars in 5 years,
with compounding.
Step 2
Now we write the future value equation for an ordinary annuity with the monthly deposits of X dollars,
compounded monthly at 5% annual interest = 12,833.59 dollars.
Thus, making monthly deposits of X dollars, we should accrue the rest 50000 - 12833.59 = 37166.41 dollars in 5 years,
with compounding.
Step 2
Now we write the future value equation for an ordinary annuity with the monthly deposits of X dollars,
compounded monthly at 5% annual interest
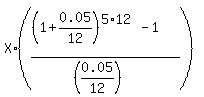 = 37166.41,
We calculate the factor/multiplier at X separately, and we get this equation
X*68.00608284 = 37166.41.
Solve for X and get the ANSWER
X = = 37166.41,
We calculate the factor/multiplier at X separately, and we get this equation
X*68.00608284 = 37166.41.
Solve for X and get the ANSWER
X = 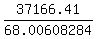 = 546.52.
At this point, the problem is solved completely.
The necessary monthly deposit is 546.52 dollars. = 546.52.
At this point, the problem is solved completely.
The necessary monthly deposit is 546.52 dollars.
Hip-hip, hurray !
|
|
|