Question 1196553: A sky diver jumps from a reasonable height above the ground. The air resistance she experiences is proportional to her velocity, and the constant of proportionality is 0.2. It can be shown that the downward velocity of the sky diver at time t is given by
𝑣(𝑡) = 54(1 − exp(−0.2𝑡))
where t is measured in seconds and 𝑣(𝑡) is measured in meters/second. The maximum velocity of a falling object with wind resistance (as 𝑡 → ∞) is called its terminal velocity. With this definition, find the maximum velocity of this sky diver.
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
As t ---> oo, 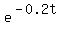 becomes small and tends to zero.
Therefore, v(t) becomes very close to 54 units and tends to 54 meters per second.
Solved and explained.
Answer by math_tutor2020(3816)  (Show Source):
You can put this solution on YOUR website!
The exp(−0.2t) can be written as e^(-0.2t) or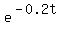
As t approaches infinity, the exp(−0.2t) will approach 0
We can see this if we made a table of values
| t | Exp(-0.2t) | | 10 | 0.1353 | | 20 | 0.0183 | | 30 | 0.0025 | | 40 | 0.0003 |
As t gets bigger, exp(−0.2t) gets closer to 0.
Or we could look at the graph of y = e^(-0.2x) to see the curve slowly approaching the x axis. It never actually arrives at the x axis.
You can use graphing tools like Desmos, GeoGebra, or a TI83 (or similar) to graph.
Since the expression exp(-0.2t) approaches zero, it basically goes away when t approaches infinity.
So the v(t) approaches 54(1-0) = 54
Answer: Terminal velocity is 54 m/s
|
|
|
