Question 1196157: Find the modulus and argument of √(1+2i)/(1-2i)
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
Answer by ikleyn(52777)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the modulus and argument of √(1+2i)/(1-2i)
~~~~~~~~~~~~~~~~~
The solution by Edwin is fine.
Another solution and another analysis is possible, which is in my post below.
It allows to get the answer with significantly less computational efforts.
So, we consider 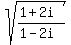 . (1)
First consider the ratio under the square root . (1)
First consider the ratio under the square root  . (2)
The numerator has the modulus |1+2i| = . (2)
The numerator has the modulus |1+2i| = 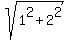 = =  .
The denominator has the modulus |1-2i| = .
The denominator has the modulus |1-2i| = 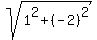 = =  .
Therefore, the ratio .
Therefore, the ratio  has the modulus of has the modulus of 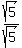 = 1.
Hence, the original complex number = 1.
Hence, the original complex number 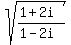 has the modulus has the modulus 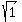 = 1.
+-----------------------------------------------+
| Thus we completed with the modulus. |
| Now, let's determine the argument of (1). |
+-----------------------------------------------+
Consider the ratio under the square root = 1.
+-----------------------------------------------+
| Thus we completed with the modulus. |
| Now, let's determine the argument of (1). |
+-----------------------------------------------+
Consider the ratio under the square root   . (3)
The numerator has the argument "a" in QI such that tan(a) = 2/1 = 2.
The denominator has the argument "b" in QIV such that tan(b) = (-2)/1 = -2.
Therefore, b = -a (which is obvious).
Hence, the ratio . (3)
The numerator has the argument "a" in QI such that tan(a) = 2/1 = 2.
The denominator has the argument "b" in QIV such that tan(b) = (-2)/1 = -2.
Therefore, b = -a (which is obvious).
Hence, the ratio  has the argument a - b = a - (-a) = 2a.
When we take square root of (3), the argument of the resulting complex number will be has the argument a - b = a - (-a) = 2a.
When we take square root of (3), the argument of the resulting complex number will be  = a.
Thus we get the ANSWER:
+----------------------------------------------------------------------------+
| the modulus of the sough complex number is 1; |
| |
| the argument of the sought complex number is "a" such that tan(a) = 2, |
| i.e. a = arctan(2) = 1.10715 radians = 63.435 degrees (rounded). |
+----------------------------------------------------------------------------+
For completeness, when we take square root of (3), we obtain, actually, two complex numbers.
First one has the argument "a", as we found it above; the second complex number has the argument a+ = a.
Thus we get the ANSWER:
+----------------------------------------------------------------------------+
| the modulus of the sough complex number is 1; |
| |
| the argument of the sought complex number is "a" such that tan(a) = 2, |
| i.e. a = arctan(2) = 1.10715 radians = 63.435 degrees (rounded). |
+----------------------------------------------------------------------------+
For completeness, when we take square root of (3), we obtain, actually, two complex numbers.
First one has the argument "a", as we found it above; the second complex number has the argument a+ .
So, the second value of the square root has the modulus of 1 and the argument arctan(2)+ .
So, the second value of the square root has the modulus of 1 and the argument arctan(2)+ = 243.435 degrees. = 243.435 degrees.
Solved.
The answer is the same as in the post by Edwin.
-----------------
On complex numbers, see relevant lessons
- Complex numbers and arithmetical operations on them
- Complex plane
- Addition and subtraction of complex numbers in complex plane
- Multiplication and division of complex numbers in complex plane
- Solved problems on taking roots of complex numbers
- Solved problems on arithmetic operations on complex numbers
- Solved problem on taking square root of complex number
in this site.
Also, you have this free of charge online textbook on ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Complex numbers".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|