Question 1193254: MAT 145: Topics In Contemporary Math
17: Exponential Growth
6) When Professor Holz’ cats were allowed outside, the population of birds and small fuzzy animals (chipmunks, squirrels, and rabbits) slowly decreased (both of his kitties are pretty good hunters!) The total population of the other animals decreased by 1% per week. If the neighborhood originally had 500 animals, how many were left after two years (104 weeks)?
Found 2 solutions by Theo, Scott713:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! a loss rate of 1% per week is equal to a growth rate of minus 1% per week.
the growth factor becomes 1 - .01 = .99 per week.
there were originally 500 animals.
after 104 weeks, the number of animals left was 500 * .99 ^ 104 = 175.8056033.
you may round up to 176 or you may round down to 175.
if you round up to 176, then the number of weeks is slightly less than 104.
if you you round down to 175, then the number of weeks is slightly more than 104.
this can be seen on the following graph.
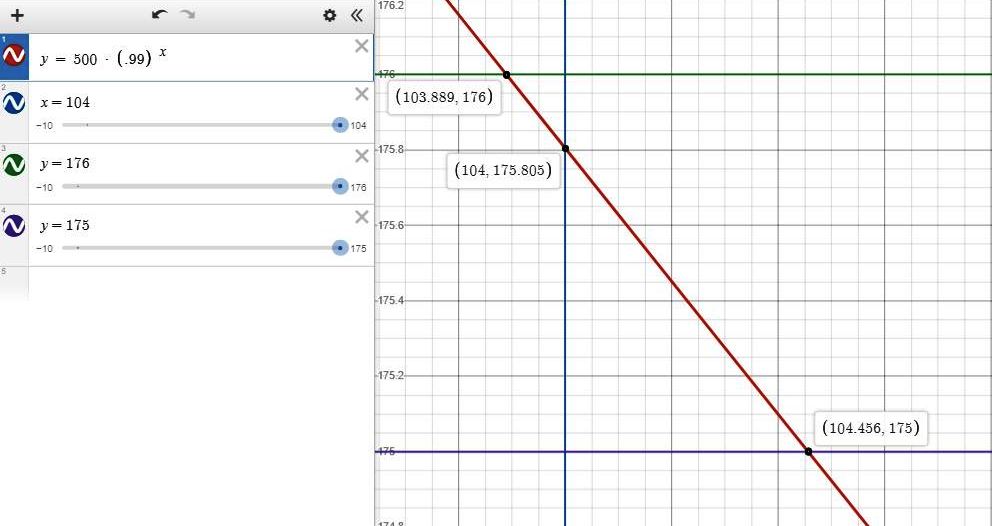
the question was:
If the neighborhood originally had 500 animals, how many were left after two years (104 weeks)?
the solution is, as best i can determine:
after 104 weeks, there were 175 animals left.
Answer by Scott713(2)   (Show Source): (Show Source):
|
|
|