Question 1168309: The sum of 128 consecutive odd, positive integers is the greatest power of two less than 200,000. The sum of the least and the greatest of these integers is 2^N. What is the value of N?
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The sum of 128 consecutive odd, positive integers is the greatest power of two less than 200,000.
The sum of the least and the greatest of these integers is 2^N. What is the value of N?
~~~~~~~~~~~~~~~
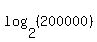 = 17.61 (approximately, with two decimals).
Therefore, the greatest power of 2 less than 200,000 is = 17.61 (approximately, with two decimals).
Therefore, the greatest power of 2 less than 200,000 is  = 131072.
So, the sum of 128 consecutive odd positive integers is 131072.
These consecutive integer numbers form an arithmetic progression;
therefore, their sum is the product of the number of terms (128) by half the sum of the least and the greatest of these two numbers.
In other words, = 131072.
So, the sum of 128 consecutive odd positive integers is 131072.
These consecutive integer numbers form an arithmetic progression;
therefore, their sum is the product of the number of terms (128) by half the sum of the least and the greatest of these two numbers.
In other words,  = =  .
It is equivalent to .
It is equivalent to
 = = 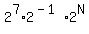 , or , or
 = = 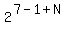 , or , or
 = = 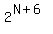 .
It implies 17 = N + 6, or N = 17 - 6 = 11.
ANSWER. N = 11. .
It implies 17 = N + 6, or N = 17 - 6 = 11.
ANSWER. N = 11.
Solved.
|
|
|