Question 1127112: If 5^678 is written as an integer, what are it's final four digits?
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! If 5^678 is written as an integer, what are it's [sic] final four digits?
---------
it's = it is
----
If by "final four" you mean the 4 least significant (on the right side):
They are: 5625
Answer by ikleyn(52785)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The table below represents the values of  in the second column, n = 1, 2, 3, 4, . . . , 20.
The third column represents the last 4 digits of the number in the second column, n = 1, 2, 3, 4, . . . , 20.
The third column represents the last 4 digits of the number  .
1 5 5
2 25 25
3 125 125
4 625 0625
5 3125 3125
6 15625 5625
7 78125 8125
8 390625 0625
9 1953125 3125
10 9765625 5625
11 48828125 8125
12 244140625 0625
13 1220703125 3125
14 6103515625 5625
15 30517578125 8125
16 152587890625 0625
17 762939453125 3125
18 3814697265625 5625
19 19073486328125 8125
20 95367431640625 0625
An experimental fact is that starting from n = 4, the last 4 digit numbers form a periodical (cyclical) sequence
with the period (the cycle length) of 4:
0625, 3125, 5625, 8125.
It can be proved mathematically. I will not prove it here - see, for example, the lesson
Find the last three digits of these numbers in this site. .
1 5 5
2 25 25
3 125 125
4 625 0625
5 3125 3125
6 15625 5625
7 78125 8125
8 390625 0625
9 1953125 3125
10 9765625 5625
11 48828125 8125
12 244140625 0625
13 1220703125 3125
14 6103515625 5625
15 30517578125 8125
16 152587890625 0625
17 762939453125 3125
18 3814697265625 5625
19 19073486328125 8125
20 95367431640625 0625
An experimental fact is that starting from n = 4, the last 4 digit numbers form a periodical (cyclical) sequence
with the period (the cycle length) of 4:
0625, 3125, 5625, 8125.
It can be proved mathematically. I will not prove it here - see, for example, the lesson
Find the last three digits of these numbers in this site.
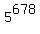 is 678-th term of this long sequence, and it is equal to the (678-3) mod 4 term of the basic cycle.
Since (678-3) mod 4 = 3, it means that the 678-th term of the long sequence is 678-th term of this long sequence, and it is equal to the (678-3) mod 4 term of the basic cycle.
Since (678-3) mod 4 = 3, it means that the 678-th term of the long sequence  is equal
to the 3-rd term of the basic cycle, i.e. 5625.
Answer. is equal
to the 3-rd term of the basic cycle, i.e. 5625.
Answer. 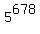 has the last four digits 5625. has the last four digits 5625.
|
|
|