Tutors Answer Your Questions about Exponents-negative-and-fractional (FREE)
Question 1053758: What are all possible factors of: 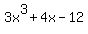
A.) 1, -1, 2, -2, 3, -3, 4, -4, 5, -5, 6, -6, 9, -9, 12, -12, 18, -18, 36, -36
B.) -1, -2, -3, -4, -6, 6, 9, 12, 18, 36
C.) 1, 2, 3, 4, 6, -6, -9, -12, -18, -36
D.) 1, -1, 2, -2, 3, -3, 1/3, -1/3, 2/3, -2/3, 4, -4, 4/3, -4/3, 6, -6, 12, -12
Click here to see answer by josgarithmetic(39623)  |
Question 1057311: This involves negative exponents and "equations quadratic in form." The equation is:
x^-4 - 10^-2 + 9 = 0 (those are negative exponents: x to the negative fourth power, etc.)
To make solving easier, a substitution is used. Let u = x^-2, and rewrite the original equation as a quadratic equation:
u^2 - 10u + 9 = 0
Factor: (u-1)(u-9) = 0
Apply the zero-product principle: u-1 = 0 or u-9 = 0; so:
u = 1 or u = 9
Now replace u with x^-2 in each of the above equations:
x^-2 = 1 or x^-2 = 9.
Get rid of the negative exponents:
1/x^2 = 1 or 1/x^2 = 9
And now here is where I get confused. At this point, my professor writes this on the board as the next step:
x^2 = 1 or x^2 = 1/9
I have no idea how he got from the previous step to this step.
From here, he goes on to apply the square root property:
x = +-1 or x = +-1/3
This is the final answer.
So my question is:
How do we get from
1/x^2 = 1 or 1/x^2 = 9
to
x^2 = 1 or x^2 = 1/9
?
Thank you for any help you can give, and my apologies for the long question.
Click here to see answer by ikleyn(52832)   |
Question 1057311: This involves negative exponents and "equations quadratic in form." The equation is:
x^-4 - 10^-2 + 9 = 0 (those are negative exponents: x to the negative fourth power, etc.)
To make solving easier, a substitution is used. Let u = x^-2, and rewrite the original equation as a quadratic equation:
u^2 - 10u + 9 = 0
Factor: (u-1)(u-9) = 0
Apply the zero-product principle: u-1 = 0 or u-9 = 0; so:
u = 1 or u = 9
Now replace u with x^-2 in each of the above equations:
x^-2 = 1 or x^-2 = 9.
Get rid of the negative exponents:
1/x^2 = 1 or 1/x^2 = 9
And now here is where I get confused. At this point, my professor writes this on the board as the next step:
x^2 = 1 or x^2 = 1/9
I have no idea how he got from the previous step to this step.
From here, he goes on to apply the square root property:
x = +-1 or x = +-1/3
This is the final answer.
So my question is:
How do we get from
1/x^2 = 1 or 1/x^2 = 9
to
x^2 = 1 or x^2 = 1/9
?
Thank you for any help you can give, and my apologies for the long question.
Click here to see answer by MathTherapy(10555)   |
Question 1059356: I need the formula for the following word problems;
Mallory has saved x half dollars. She has four times as many quarters as half-dollars. The total she saved is $61.50. How many half-dollars does she have? How many quarters does she have?
Tony, Dominic, and Joseph purchased a sub sandwich. Tony ate 1/4 of the pieces. Dominic and Joseph each ate 1/6 of the pieces. There are 5 pieces left. How many total pieces were there originally?
Click here to see answer by jorel555(1290)  |
Question 1061972: Simplifying without a calculator using the rules of exponents. Showing work and putting in a^u b^2 format
a^2x b^-x (a^x)^4 (b^2)^x (1/a)^3
^^^all one problem a & b were not put in parenthesis with their separate exponents and this is exactly how it was written, to avoid any confusion.
I'm not sure where to start or how to break down this problem.
Click here to see answer by MathTherapy(10555)   |
Question 1067084: The population of the United States has been changing at an exponential rate since the year 2000. The function P(t)=282(1.35)^t, where P(t) is the population after t years, models the country's growth. Determine the initial value, a, and the base, b. Then, determine whether this function represents exponential growth or exponential decay, and the rate of growth or decay.
Click here to see answer by stanbon(75887)  |
Question 1067083: A microbiologist is studying a new strain of flesh-eating bacteria that can be found in oceans around the world. After collecting a year’s worth of data about the time it takes for the bacteria to replicate, she determines the following function b(t)=45.4(5.69)^t, where b(t) is the amount of bacteria in parts per thousand per day, t. What is the a value and what does it mean in terms of the problem situation?
Click here to see answer by stanbon(75887)  |
Question 1067224: Jennifer starts a new investment account that grows exponentially. Her financial advisor tells her the initial investment of $50,000 grows at a rate of about 15% annually.
1. Determine a function, I(t), that determines Jennifer’s investment account balance after t years. For the exponential growth function, what are the “a” and “b” values? What do those values represent? (5 points for the explanation of “a” and “b” and 5 points for the function)
2. Calculate how much money Jennifer will have after 10 years. (10 points)
3. What is Jennifer was able to deposit $100,000 as her initial investment, instead of $50,000.
Write a new function, N(t), to show this change. (3 points)
Calculate how much money Jennifer would have after 8 years. (2 points)
Using complete sentences, compare the differences in the functions and the amount of money after 8 years for the two different functions. (5 points)
4. Graph the function I(t) and identify the y-intercept and the equation of the asymptote. (5 pts)
5. Graph the function N(t) and identify the y-intercept and the equation of the asymptote. (5 pts)
6. What does the asymptote mean in terms of Jennifer’s investment account? Be sure to explain your reasoning for credit. (5 pt)
7. Due to a worldwide recession, Jennifer’s financial advisor informs her the account is no longer growing after 4 years. He recommends she move her money to an account that is more conservative and earns only 4% annually. Determine the amount in Jennifer’s investment account after 4 years(using the $50,000 investment), rounding to the nearest dollar. It may be helpful to create a table. (10 points)
8. Write a new function, N(t), that represents the amount of money in Jennifer’s new account after t years. Be sure to use correct notation. (5 pts)
9. Did the asymptote of the new function change due to Jennifer moving her investment? Explain your reasoning. (5 pts)
Part II:
10. Determine the area of a rectangle whose length is expressed as 3x3y2 and the width is expressed as 5x2y4. (5 points)
11. Determine the volume for a prism whose length is expressed as 3x3y2 and the width is expressed as 5x2y4 and a height of 2xy2 (5 points)
Part III. Sequences
A national pool tournament starts with 650 teams. Each round sends half the teams to the losers bracket.
12. Complete the table below to show the number of teams in the tournament (5 points)
13. Write an explicit formula to describe this sequence that will determine how many teams are playing at any given round. Describe what “a” and “r” represent. (10 points)
15. How are linear and exponential functions similar and different. Discuss the relationship between the m and b in y= mx+b and the a and b or a and r in y = a (b)x or an = a1(r)x. (5 points)
Click here to see answer by addingup(3677)   |
Question 1067161: Jennifer starts a new investment account that grows exponentially. Her financial advisor tells her the initial investment of $50,000 grows at a rate of about 15% annually.
1. Determine a function, I(t), that determines Jennifer’s investment account balance after t years. For the exponential growth function, what are the “a” and “b” values? What do those values represent? (5 points for the explanation of “a” and “b” and 5 points for the function)
2. Calculate how much money Jennifer will have after 10 years. (10 points)
Click here to see answer by Boreal(15235)   |
Question 1068156: Jennifer starts a new investment account that grows exponentially. Her financial advisor tells her the initial investment of $50,000 grows at a rate of about 15% annually.
1. Determine a function, I(t), that determines Jennifer’s investment account balance after t years. For the exponential growth function, what are the “a” and “b” values? What do those values represent? (5 points for the explanation of “a” and “b” and 5 points for the function)
answer:15000*(1+0.15)t
2. Calculate how much money Jennifer will have after 10 years. (10 points)
answer:$60683.366036
3. What if Jennifer was able to deposit $100,000 as her initial investment, instead of $50,000.
Write a new function, N(t), to show this change. (3 points)
answer:100000*(1+0.15)t
Calculate how much money Jennifer would have after 8 years. (2 points)
answer:$305902.286254
Using complete sentences, compare the differences in the functions and the amount of money after 8 years for the two different functions. (5 points)
answer:??
Click here to see answer by Boreal(15235)   |
Question 1068159: A national pool tournament starts with 650 teams. Each round sends half the teams to the losers bracket.
12. Complete the table below to show the number of teams in the tournament (5 points)
Answer:??
13. Write an explicit formula to describe this sequence that will determine how many teams are playing at any given round. Describe what “a” and “r” represent. (10 points)
Answer:??
14. How many rounds will it take to get down to the winning team? You may choose to use a table or a regression equation to generate a table. (5 points)
15. How are linear and exponential functions similar and different. Discuss the relationship between the m and b in y= mx+b and the a and b or a and r in y = a (b)x or an = a1(r)x. (5 points)
Answer: ??
Click here to see answer by stanbon(75887)  |
Question 1068162: Jennifer starts a new investment account that grows exponentially. Her financial advisor tells her the initial investment of $50,000 grows at a rate of about 15% annually.
1. Determine a function, I(t), that determines Jennifer’s investment account balance after t years. For the exponential growth function, what are the “a” and “b” values? What do those values represent? (5 points for the explanation of “a” and “b” and 5 points for the function)
Answer: 15000*(1+0.15)t
2. Calculate how much money Jennifer will have after 10 years. (10 points)
Answer: $60683.366036
3. What if Jennifer was able to deposit $100,000 as her initial investment, instead of $50,000.
Write a new function, N(t), to show this change. (3 points)
Answer: 100000*(1+0.15)t
Calculate how much money Jennifer would have after 8 years. (2 points)
Answer: $305902.286254
Using complete sentences, compare the differences in the functions and the amount of money after 8 years for the two different functions. (5 points)
Answer: y=ab^x, where a here is the amount deposited, and x is the number of compoundings. I'd round to two decimal places, since it is money. The figures are correct. The second is more than the first because more was deposited. The tripling time of money in years is ln3/interest rate as decimal number, because p/po=e^rt and ln (3), which is the ratio=rt, so ln3/r=t here in 10 years ln3/.15=7.32 years so that tripling just occurs for the second, but the first has quadrupled. Quadrupling is doubling of doubling, and the rule of 70 is used there, where 70 over the rate (in per cent) is the doubling time--70/15=4.67 years, so this doubled and again doubled. That is consistent with $60,000.
4. Graph the function I(t) and identify the y-intercept and the equation of the asymptote. (5 pts)
Answer: The y-intercept is (0,15,000)
The asymptote is y=0 (negative x, negative exponent, term goes to 0)
5. Graph the function N(t) and identify the y-intercept and the equation of the asymptote. (5 pts)\
Answer: y-intercept of (0,100000) and asymptote of y=0 (negative x, negative exponent, term goes to 0)
6. What does the asymptote mean in terms of Jennifer’s investment account? Be sure to explain your reasoning for credit. (5 pt)
Answer:??
7. Due to a worldwide recession, Jennifer’s financial advisor informs her the account is no longer growing after 4 years. He recommends she move her money to an account that is more conservative and earns only 4% annually. Determine the amount in Jennifer’s investment account after 4 years(using the $50,000 investment), rounding to the nearest dollar. It may be helpful to create a table. (10 points)
Answer:??
8. Write a new function, N(t), that represents the amount of money in Jennifer’s new account after t years. Be sure to use correct notation. (5 pts)
Answer:??
9. Did the asymptote of the new function change due to Jennifer moving her investment? Explain your reasoning. (5 pts)
Answer:??
can you please answer questions 6-9?
Click here to see answer by Boreal(15235)   |
Question 1068160: 10. Determine the area of a rectangle whose length is expressed as 3x3y2 and the width is expressed as 5x2y4. (5 points)
Answer:
11. Determine the volume for a prism whose length is expressed as 3x3y2 and the width is expressed as 5x2y4 and a height of 2xy2 (5 points)
Answer:
Click here to see answer by Fombitz(32388)   |
Question 1068490: Use the polynomial 6x2 7x 5for questions 6-9.
6. A piece of luggage has a base whose area is 6x2 7x5. The width of the luggage is 2x1, what is the length?
7. What is the volume of this same piece of luggage if its height is x 1? Remember: Volume= (length)(width)(height)
8. A cube shaped suitcase has a length of 3x 2 units. What is an expression for its area of the base?
9. What is the volume of this cube shaped luggage?
Click here to see answer by Alan3354(69443)   |
Question 1069457: 1 Which of the following describes the process you should take to find the factors of x^2+9x+8
a. Find two numbers that multiply to equal 72 and add to equal 17.
b. Find two numbers that multiply to equal 8 and add to equal 9
c. Find two numbers that divide to equal 8 and subtract to equal 9.
d. Find two numbers that multiply to equal 9 and add to equal 8.
5. Factor the GCF from the following polynomial: -5x^2+10x^4+25x
answer:??
7. Factor the GCF from the following polynomial: 18x^2+3x^3-12x^5
answer:??
9. Factor the following polynomial, including any greatest common factors and write in simplified factored form: 3x^3-18x^2+27x
answer:??
Click here to see answer by Boreal(15235)   |
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330
|





