Question 811685: simplify the compound fraction and show work:
1/(x+1) +1/2
over
3/(2x^2 +4x +2)
Found 2 solutions by brysca, MathTherapy:
Answer by brysca(112)   (Show Source): (Show Source):
You can put this solution on YOUR website! I gave it a shot. It looks right and I'm pretty sure it's right but I'm sorry if it's not.
First, combine the 1 and the .5 in the denominator
x+1+.5
=x+1.5
So the question translates to this:
1/(x+1.5) divided by 3/(2x^2 +4x +2)
So whenever you divide by a fraction, you multiply by its inverse instead so it looks like this:
1/(x+1.5) * (2x^2 +4x +2)/3
(2x^2 +4x +2) simplifies to (x+1)(2x+2) so you rewrite it like this
1/(x+1.5) * (x+1)(2x+2)/3
You should get something like this when multiplied:
(x+1)(2x+2)/(3x+4.5)
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! simplify the compound fraction and show work:
1/(x+1) +1/2
over
3/(2x^2 +4x +2)

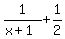 ÷ ÷ 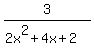
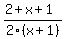 ÷ ÷ 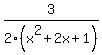
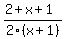 ÷ ÷ 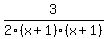
 * * 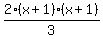
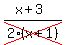 * * 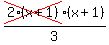
 , or , or 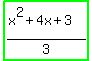
You can do the check!!
Send comments, “thank-yous,” and inquiries to “D” at MathMadEzy@aol.com. Further help is available, online or in-person, for a fee, obviously.
For FREE info and answers to questions about the ASVAB exam, the NYS 3 – 8 city/state wide exams, GENERAL MATH QUESTIONS, MATH HOMEWORK QUESTIONS, or MATH QUESTIONS related to the Regents Integrated Algebra, Regents Geometry, Regents Algebra 2/Trigonometry, SHSAT, COOP/HSPT/TACHS, PSAT, SAT, ACT, SSAT/ISEE, GRE, CLEP, and the GED, you can visit: http://asvabstudyzone.freeforums.net/.
|
|
|