1. 17 degrees 49 minutes and 10 seconds added to 22 degrees 22 minutes and 59 seconds, equals to?
17° 49' 10"
+22° 22' 59"
39° 71' 69"
Subtract 60" from 69" and get 9". Add 1' to the 71' and get 72'.
So now you have:
39° 72' 9"
Next subtract 60' from 72' and get 12'. Add 1° to the 39° and get 40°.
So you end up with
40° 12' 9"
2. To what power must 10 be raised to equal 100,000?
Count the zeros in 100,000. There are 5 of them. Therefore
105 = 100,000. Answer: the fifth power.
3. Area of a right circular cone of base radius r, and height l, is
A cone has two dimensions that are both called "heigths". Ususlly l is for the lateral height, and h for the actual height. So I'm not sure what you mean, since you just said "height" but used l.
The lateral surface area of a right circular cone is 
where 
is the radius of the circle at the bottom of the cone and 
is the lateral height of the cone (given by the Pythagorean theorem 
where 
is the actual height of the cone). The surface area of the bottom circle of a cone is the same as for any circle, 
. Thus the total surface area of a right circular cone is:
or
4.The supplement of 13 degrees is
180° - 13° = 167°
5. 64y = 64
Divide both sides by 64
= 
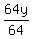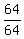Cancel the 64's onthe left and divide on the right:
=
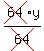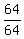or y = 1
Edwin
