Question 430664: evaluate 243^(-2/5) without a calculator
Found 2 solutions by jsmallt9, Gersid:
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website!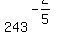 
If you have trouble with negative and/or fractional exponents I find that it can be helpful to factor the exponent is a certain way:- If the exponent is negative, factor out a -1.
- If the exponent is fractional and the numerator is not a 1, then factor out the numerator.
Let's see this in action:
1) Your exponent is negative so we factor out -1:
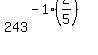
2) Your exponent is fractional and the numerator is 2, so we will factor out 2:
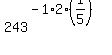
With the exponent factored, each factor tells us an operation to perform:- The -1, as an exponent, tells us to find a reciprocal.
- The 2, as an exponent, tells us to square something
- The 1/5, as an exponent, tells us to find a 5th root.
And since multiplication is Commutative, we can rearrange the order of the factors in any way we choose. So let's figure out an order that seems to make the whole process easiest. (Note: Any order, if done correctly, will work and give us the right answer. So you don't have to agree with the order I am going to choose.)
Since a reciprocal of a whole number creates a fraction, I'm not going to start with a reciprocal. And squaring 243 will create a very large number. So I'm going to pospone squaring, too. Normally a 5th root would seem the least appealing operation of all. But with a little investigation we can find that  , so a 5th root of 243 actually looks like a good place to start. It will create a small number that will be easy to square. And last we'll find a reciprocal:
Rearranging the factors into the desired order:
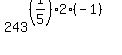
Using the  rule (in reverse):
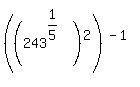
Simplifying:
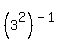
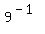
Answer by Gersid(33) (Show Source):
|
|
|
