Question 396287: 3(x+1)^(4/3)=48
Answer by jsmallt9(3758)   (Show Source):
You can put this solution on YOUR website! 
First let's isolate the base, (x+1), and its exponent, 4/3, on one side of the equation by dividing both sides by 3:
Next we want to find a way to change the exponent from 4/3 to a 1. We can do so by combining all of the following ideas:- One is allowed to raise both sides of an equation to any non-zero power.
- The rule for exponents when raising a power to a power is to multiply the exponents.
- Multiplying reciprocals always results in a 1.
All of this tells us that if we raise each side of the equation to the reciprocal of 4/3 power, we will end up with an exponent of 1 on the left side. The reciprocal of 4/3 is 3/4:
On the left side the exponent turns into a 1, as planned:
Simplifying the left side is simple. The right side is not so simple. If you have trouble with negative or fractional exponents I find it can be helpful to factor the exponent in a certain way:- If the exponent is negative, factor out a -1.
- If the exponent is fractional and if the numerator is not a 1, then factor out the numerator. (You'll see what this means in a moment.)
The exponent on the right is not negative but it is a fraction whose numerator is not a 1. So we will factor out the 3:
Now, looking at the exponent in factored form, the 3 tells us we will be cubing and the 1/4 tells us that we will be finding a 4th root. And we can do these two operations in any order! Normally 4th roots aren't simple. However, since  , finding the 4th root of 16 is rather easy. So we will start with the 4th root and then cube it:
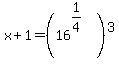
x+1 = 8
Now we just subtract 1:
x = 7
|
|
|
