SOLUTION: For my sheet of notes, I need to solve for "x." The problem given is: {{{4x^2(2^x)-9(2^x)=0}}} Another one that's given is {{{8x^(x+1) =32sqrt( 2 )}}} I've tried these pro

Algebra ->  Exponents-negative-and-fractional -> SOLUTION: For my sheet of notes, I need to solve for "x." The problem given is: {{{4x^2(2^x)-9(2^x)=0}}} Another one that's given is {{{8x^(x+1) =32sqrt( 2 )}}} I've tried these pro      Log On


   

Question 365274: For my sheet of notes, I need to solve for "x." The problem given is:
4x%5E2%282%5Ex%29-9%282%5Ex%29=0
Another one that's given is 8x%5E%28x%2B1%29+=32sqrt%28+2+%29
I've tried these problems over and over, but I can't figure them out. Please, help me!
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
4x%5E2%282%5Ex%29-9%282%5Ex%29=0
With an equation like this, one way to solve it is to get one side equal to zero and then factor it. One side of this equation is alrady zero so we can go straight to factoring.

When fctoring, always start with the Greatest common factor (GCF). The GCF here is 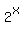2%5Ex:
%282%5Ex%29%284x%5E2+-9%29+=+0
Next we can factor using the difference of squares pattern, a%5E2+-+b%5E2+=+%28a%2Bb%29%28a-b%29:
%282%5Ex%29%282x+%2B+3%29%282x+-+3%29+=+0
We now have factored the left side as much as possible. Next we use the Zero Product Property which tells us that this product can be zero only if one of the factors is zero. So:
2%5Ex+=+0 or 2x + 3 = 0 or 2x - 3 = 0
Now we solve these. Since a power of 2 can never be zero, the first of these equations has no solution. But the other two equations can be solved. We end up with:
x = 3/2 or x = -3/2

8x%5E%28x%2B1%29+=32sqrt%28+2+%29
As this was posted, I can't find a solution, either. All I can say is that a good first step would be to divide both sides by 8:
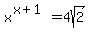
x%5E%28x%2B1%29+=+4sqrt%28+2+%29
From here I'm not sure where to go. One could rewrite the right side as a power of 2:
x%5E%28x%2B1%29+=+2%5E2%2A2%5E%281%2F2%29
x%5E%28x%2B1%29+=+2%5E%282%2B%281%2F2%29%29
x%5E%28x%2B1%29+=+2%5E%285%2F2%29
Having both sides as exponential expressions may help but I'm not seeing how yet.

If, by chance, the equation was actually
8%5E%28x%2B1%29+=32sqrt%28+2+%29
Then rewriting each side as a power of 2 leads to a solution:
%282%5E3%29%5E%28x%2B1%29+=+2%5E5%2A2%5E%281%2F2%29
2%5E%283x%2B3%29+=+2%5E%285%2B%281%2F2%29%29
2%5E%283x%2B3%29+=+2%5E%2811%2F2%29
With each side a power of 2, the exponents must be equal in order for the powers of 2 to be equal, So:
3x%2B3+=+11%2F2
This is a simple equation to solve. First we'll eliminate the fraction by multiplying both sides bby 2:
6x + 6 = 11
Subtract 6 from each side:
6x = 5
Divide both sides by 6:
x+=+5%2F6