SOLUTION: (4x to the negative one power, y to the 1/3 power) to the 3/2 power ___________ ___________ ___________ ___________ ___________ _______(over) (xy) to the 3/2

Algebra ->  Exponents-negative-and-fractional -> SOLUTION: (4x to the negative one power, y to the 1/3 power) to the 3/2 power ___________ ___________ ___________ ___________ ___________ _______(over) (xy) to the 3/2       Log On


   

Question 214257This question is from textbook
: (4x to the negative one power, y to the 1/3 power) to the 3/2 power
___________________________________________________________________(over)
(xy) to the 3/2 power


I really need help with this one, I don't understand it at all... This question is from textbook

Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!

When working with exponents there are several key things to understand:
  • The rules for exponents:
    1. a%5Ep+%2A+a%5Eq+=+a%5E%28p%2Bq%29
    2. a%5Ep%2Fa%5Eq+=+a%5E%28p-q%29
    3. %28a%5Ep%29%5Eq+=+a%5E%28p%2Aq%29
    4. %28a%2Ab%29%5Ep+=+a%5Ep+%2A+b%5Eq
    5. %28a%2Fb%29%5Ep+=+%28a%5Ep%29%2F%28b%5Ep%29
    6. a%5E%281%2Fp%29+=+root%28p%2C+a%29
    7. a%5E%28-p%29+=+1%2F%28a%5Ep%29
    8. a%5E0+=+1 (if a is not zero)
  • The rules above apply regardless what the exponents are. They work on positive, negative, zero and fractional exponents.
  • As with most things in Math, the rules work in both directions.
  • Since exponents are, in essence, a form of multiplication and since multiplication is commutative, it rarely makes a difference the order you apply these rules (as long as you apply them correctly!).

So there are often many ways to simplify an expression with exponents. Here's a couple of possible solutions:

Solution #1:

1) Using rule #4 on the numerator and on the denominator:
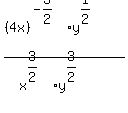
%28%284x%29%5E%28-3%2F2%29%2Ay%5E%281%2F2%29%29%2F%28x%5E%283%2F2%29%2Ay%5E%283%2F2%29%29
2) Using rule #4 on the "4x":

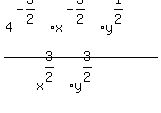
3) Using rule #2 on the x's and y's"
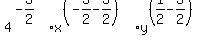
4%5E%28-3%2F2%29%2Ax%5E%28%28-3%2F2+-+3%2F2%29%29%2Ay%5E%28%281%2F2+-+3%2F2%29%29
which simplifies to
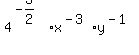
4%5E%28-3%2F2%29%2Ax%5E%28-3%29%2Ay%5E%28-1%29
4) To simplify the 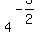4%5E%28-3%2F2%29, if you don't see it otherwise, factor the exponent:
4%5E%283%2A%281%2F2%29%2A%28-1%29%29%2Ax%5E%28-3%29%2Ay%5E%28-1%29
5) Then we can use rule #3 (from right to left) twice:
%28%284%5E3%29%5E%281%2F2%29%29%5E%28-1%29%29%2Ax%5E%28-3%29%2Ay%5E%28-1%29
6) Since 4^3 = 64:
%28%2864%29%5E%281%2F2%29%29%5E%28-1%29%29%2Ax%5E%28-3%29%2Ay%5E%28-1%29
7) Using rule #6 on 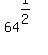64%5E%281%2F2%29"
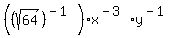
%28%28sqrt%2864%29%29%5E%28-1%29%29%2Ax%5E%28-3%29%2Ay%5E%28-1%29
8) Since sqrt%2864%29+=+8:
8%5E%28-1%29%2Ax%5E%28-3%29%2Ay%5E%28-1%29
9) Using rule #7 on 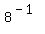8%5E%28-1%29:
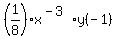
%281%2F8%29%2Ax%5E%28-3%29%2Ay%28-1%29
At this point we could stop, unless you are not supposed to have negative exponents, In this case we use rule 9 on the x's and y's giving:
1%2F%288x%5E3y%29

Solution #2:

1) Use Rule #5 (from right to left) on the entire fraction (since the exponents on the numerator and denominator are the same):
%28%28%284x%29%5E%28-1%29%2Ay%5E%281%2F3%29%29%2F%28xy%29%29%5E%283%2F2%29%29
2) Using rule #4 on the "4x":
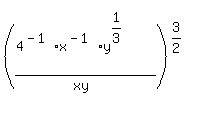
%28%284%5E%28-1%29%2Ax%5E%28-1%29%2Ay%5E%281%2F3%29%29%2F%28xy%29%29%5E%283%2F2%29
3) Using rule #2 on the x's and y's"
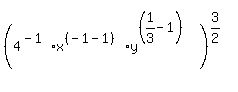
%284%5E%28-1%29%2Ax%5E%28%28-1-1%29%29%2Ay%5E%28%281%2F3-1%29%29%29%5E%283%2F2%29
which simplifies to
%284%5E%28-1%29%2Ax%5E%28-2%29%2Ay%5E%28-2%2F3%29%29%5E%283%2F2%29
4) Using rule #3:
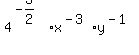
4%5E%28-3%2F2%29%2Ax%5E%28-3%29%2Ay%5E%28-1%29
And the rest is the same as the first solution....