SOLUTION: Assume there is a certain population of fish in a pond whose growth is described by the logistic equation. It is estimated that the carrying capacity for the pond is 1600 fish. Abs

Algebra ->  Exponents-negative-and-fractional -> SOLUTION: Assume there is a certain population of fish in a pond whose growth is described by the logistic equation. It is estimated that the carrying capacity for the pond is 1600 fish. Abs      Log On


   

Question 1206141: Assume there is a certain population of fish in a pond whose growth is described by the logistic equation. It is estimated that the carrying capacity for the pond is 1600 fish. Absent constraints, the population would grow by 120% per year.
If the starting population is given by ,p0=200 then after one breeding season the population of the pond is given by
P1=
after two breeding seasons the population of the pond is given by
P2=
Answer by ikleyn(52834) About Me  (Show Source):
You can put this solution on YOUR website!
.
Assume there is a certain population of fish in a pond whose growth is described by the logistic equation.
It is estimated that the carrying capacity for the pond is 1600 fish. Absent constraints,
the population would grow by 120% per year.
If the starting population is given by p0=200, then estimate population of fish in the pond
after one and two years.
~~~~~~~~~~~~~~~~~~~~~


One good Internet source to read and to learn about a logistic equation is Libre text
https://math.libretexts.org/Bookshelves/Calculus/Calculus_(OpenStax)/08%3A_Introduction_to_Differential_Equations/8.04%3A_The_Logistic_Equation 


The general solution for the standard logistic differential equation is so called logistic function

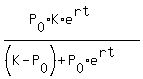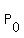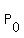    P(t) = %28P%5B0%5D%2AK%2Ae%5E%28rt%29%29%2F%28%28K-P%5B0%5D%29%2BP%5B0%5D%2Ae%5E%28rt%29%29.


Here P%5B0%5D is the initial population, P(t) is current population, K is the carrying capacity 
and "r" is growth rate. Number "e" = 2.71828 is the base of natural logarithm 
(shown here as an approximate value).


In this current problem in the post, we are given

    P%5B0%5D = 200,  K = 1600,  r = 1.2.


They want you determine P(1) and P(2), the population after 1 and 2 years.


(a)  For t = 1 year

     P(1) = %28200%2A1600%2Ae%5E%281.2%2A1%29%29%2F%28%281600-200%29%2B200%2Ae%5E%281.2%2A1%29%29 = 514.74,  or 514  (rounded).


(b)  For t = 2 years

     P(2) = %28200%2A1600%2Ae%5E%281.2%2A2%29%29%2F%28%281600-200%29%2B200%2Ae%5E%281.2%2A2%29%29 = 978.58,  or  979  (rounded).

Solved.

-------------------

Post-solution notice 
    In my opinion, the question in the post is posed/worded INCORRECTLY.

    It asks about the breeding season, but we are not given information
    for a breading season - we are given information, related to years - so,
    the question should be about the times of years, not the breeding seasons.

    The life of fish includes not only breeding - it includes also struggle for food, 
    survival from predators and diseases, natural death, that is, processes with a period of a year.