Question 1202091: why -2 to the power of 4 = -16?
Found 4 solutions by ikleyn, MathTherapy, math_tutor2020, greenestamps:
Answer by ikleyn(53426)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
why -2 to the power of 4 = -16?
~~~~~~~~~~~~~~~~
-2 to the power of 4 is not -16.
-2 to the power of 4 is 16.
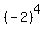 = (-2)*(-2)*(-2)*(-2) = 16. ANSWER = (-2)*(-2)*(-2)*(-2) = 16. ANSWER
Answer by MathTherapy(10587)   (Show Source): (Show Source):
You can put this solution on YOUR website!
why -2 to the power of 4 = - 16?
- 24 = (- 2)4 is NOT equal to - 16
However, it CAN BE if it's written a certain way. Can you determine that way?
Answer by math_tutor2020(3828)   (Show Source): (Show Source):
You can put this solution on YOUR website!
It's a matter of order of operations (PEMDAS)
If we write (-2)^4, then
(-2)^4 = (-2)*(-2)*(-2)*(-2) = 16
The (-2)^4 means "multiply four copies of (-2) together to get 16"
The four negatives pair up and cancel out
negative * negative = positive
If on the other hand we have -(2^4), then,
-(2)^4 = -(2)*(2)*(2)*(2) = -16
The key difference this time is the negative doesn't get copied four times
We evaluate 2^4 first, then stick a negative at the front, to end up with -16.
Recall that PEMDAS has us do the parenthesis part first, then multiplication later. Think of -(2^4) as -1*(2^4)
Side note: many calculators will interpret -2^4 as -(2^4) and not as (-2)^4
Answer by greenestamps(13258)   (Show Source): (Show Source):
You can put this solution on YOUR website!
When the expression is written in words, instead of with formal mathematical symbols, there are two different interpretations that give different answers.
(-2) to the power of 4 = (-2)^4 = 16
-(2 to the power of 4) = -(2^4) = -16
|
|
|