Question 1136383: This is my latest problem if some one may wish to kindly share i hope i have done the following correctly (5*y^2-7*y+1)/(y-1) this is changing a fraction into a mixed expression i have seen the step by step answer, im aware that a similarity to long division is done here. But im a bit baffelled how -1 is the numerator to part of the final answer, may someone please clearly state how this is achieved Kind regards mike.
Found 2 solutions by MathLover1, MathTherapy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by MathTherapy(10555)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is my latest problem if some one may wish to kindly share i hope i have done the following correctly (5*y^2-7*y+1)/(y-1) this is changing a fraction into a mixed expression i have seen the step by step answer, im aware that a similarity to long division is done here. But im a bit baffelled how -1 is the numerator to part of the final answer, may someone please clearly state how this is achieved Kind regards mike.
It's very similar to converting an IMPROPER FRACTION such as 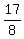 , to a MIXED NUMBER. , to a MIXED NUMBER.
Dividing 17 (numerator) by 8 (denominator) gives 2, the WHOLE-NUMBER QUOTIENT, and with ONE (1) being the REMAINDER,
it's placed over the DENOMINATOR, or DIVISOR, which is 8. This gives us the MIXED NUMBER final-answer: 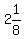 . .
For this problem, after DIVIDING out  , we get the QUOTIENT 5y - 2, and the REMAINDER, - 1. , we get the QUOTIENT 5y - 2, and the REMAINDER, - 1.
Along with the DIVISOR, or DENOMINATOR, y - 1, we get a final answer of: 
|
|
|