Tutors Answer Your Questions about Exponential-and-logarithmic-functions (FREE)
Question 1178434: Total emissions of carbon dioxide from the burning of fossil fuels have been increasing at about 3% per year (data from 2010 to 2011). If emissions continue to increase at this rate, about how much higher will total emissions be in 2035 than in 2010?
Click here to see answer by Boreal(15235)   |
Question 1178811: Please help me solve this!
Use properties of logarithms to expand the logarithmic expression as much as possible. Where possible, evaluate logarithmic expressions without using a calculator.
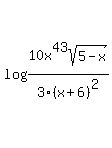
The top row is 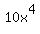 next to the sqrt not 43 as it appears. Thanks so much! next to the sqrt not 43 as it appears. Thanks so much!
Click here to see answer by Edwin McCravy(20059)   |
Question 1178978: A biologist finds that a local habitat has a population of 10 raccoons. The population of the
raccoons grows according to the model P = 10(1.054)t. What will be the population of raccoons in this habitat in 8 years?
Click here to see answer by ikleyn(52800)   |
Question 1178980: 24 grams of a radioactive isotope whose half-life is 1430 years decays according to the model
A = 24(1/2) ^ (t/1430) where A is the amount remaining after t years. How many years will it take
until 20 grams remain?
Click here to see answer by ikleyn(52800)   |
Question 1178977: After taking his last college Latin course in 2005, Harold knows approximately 20,000
words. Unfortunately, the number of words he remembers decreases according to the model
W = 20000(0.904)t where W is the number of words he remembers t years after 2005. How
long before Harold knows only half of the words he learned in college?
Click here to see answer by ikleyn(52800)   |
Question 1178996: The alkalinity of a fluid (pH) can be modeled in terms of its hydrogen ion concentration (H+
, measured in moles/liter) of the fluid using the model shown below:
Ph = -log(H^+)
A lab technician finds that a sample of fluid has a pH of 4.5. What is the hydrogen ion
concentration of the fluid?
Click here to see answer by josgarithmetic(39620)  |
Question 1178981: Abe deposits $1500 into a savings account that pays 1.96% per year for t years. How long
before the amount doubles if…
a. the interest is compounded quarterly (n = 4) using A= P (1+r/n)^nt?
b. the interest is compounded continuously using A= Pe^rt?
c. What is the annual percent yield on this deposit if it is compounding continuously?
Click here to see answer by Theo(13342)   |
Question 1179397: there are currently 100,000 people in a stadium watching a soccer game. when the game ends, about 3% of the crowd will leave the stadium each minute. at this rate, how many minutes will it take for 3/4 of the crowd to leave the stadium
pls help and have step by step if u can i am so confused with this lesson :(
Click here to see answer by MathLover1(20850)   |
Question 1179397: there are currently 100,000 people in a stadium watching a soccer game. when the game ends, about 3% of the crowd will leave the stadium each minute. at this rate, how many minutes will it take for 3/4 of the crowd to leave the stadium
pls help and have step by step if u can i am so confused with this lesson :(
Click here to see answer by MathTherapy(10552)   |
Question 1179745: A city is growing at the rate of 0.3% annually. If there were 2,520,000 residents in the city in 1993, find how many (to the nearest ten-thousand) are living in that city in 2000. Use Use y = 2,520.000(2.7)0.003t.
Click here to see answer by ikleyn(52800)   |
Question 1180107: The generation time G for a particular bacterium is the time it takes for the population to double. The bacteria increase in population is shown by the formula G = t over 3.3log a p, where t is the time period of the population increase, a is the number of bacteria at the beginning of the time period, and P is the number of bacteria at the end of the time period. If the generation time for the bacteria is 6 hours, how long will it take 8 of these bacteria to multiply into a colony of 7681 bacteria?
pls add step by step im very confused thank u for help
Click here to see answer by ikleyn(52800)   |
Question 1180630: The table below provides the average monthly temperature in London, England over the course of a year
Months Temperature (in degree)
1 January 7 degree
2 February 7.5 degree
3 March 9 degree
4 April 11 degree
5 May 14 degree
6 June 17 degree
7 July 19.5 degree
8 August 19 degree
9 September 16.5 degree
10 October 13 degree
11 November 9.5 degree
12 December 7 degree
a. Determine the equation of a sinusoidal regression function that best models the data. Express the values of a, b, c, and d to the nearest hundredth.
b. Use the sinusoidal regression equation above to predict the average temperature, to the nearest hundredth, in London next February.
c. Most tourists visit London during months when the average temperature is 13 °C and higher. Determine the month of the year when the temperature first reaches 13 °C.
Click here to see answer by ikleyn(52800)   |
Question 1182266: Which example below represents exponential decay?
A. The balance on your city bus pass if you ride the bus twice a day every day.
B. The number of views a popular (Tik Tok) gets over time
C. The number of teams competing as a tournament progresses
D. The growth of an invasive species of plants.
Click here to see answer by math_tutor2020(3817)  |
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910
|


