Tutors Answer Your Questions about Exponential-and-logarithmic-functions (FREE)
Question 1068947: This question is about logs and I don't understand it at all can you please help me solve this equation: Solve the following  . .
So far I have 
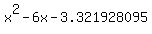
Now, I'm stuck and I'm not sure if I answered the question or if there is more work to be shown?
Get back to me as soon as possible, thank you soo much and have a nice day/night!
Click here to see answer by josgarithmetic(39620)  |
Question 1068947: This question is about logs and I don't understand it at all can you please help me solve this equation: Solve the following  . .
So far I have 
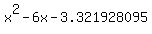
Now, I'm stuck and I'm not sure if I answered the question or if there is more work to be shown?
Get back to me as soon as possible, thank you soo much and have a nice day/night!
Click here to see answer by MathTherapy(10552)   |
Question 1069103: ``a tube with a diameter of 2 cm runs through the center of a container that is 10x10x10cm. how many cubic cm of space are left in the container?
A. 874.4 cm^3
B. 996.9 cm^3
C. 68.6 cm^3
D. 968.6 cm^3''.
''.
Click here to see answer by Boreal(15235)   |
Question 1069444: (log3 (6))/3 + (log3 (11))/3 + (log3 (5))/3
I am supposed to condense, but we never talked about working with an expression "all over" another number. Is it the same as 1/3 (log3 6) + 1/3 (log3 11) + 1/3 (log3 5)?
When this assignment was introduced, we had not talked about changing log bases or anything like that, but is that involved?
Thank you!
Click here to see answer by Alan3354(69443)   |
Question 1069541: 1. log x - log (x+2)=1
2. (4^x)-40=3*2^x
3.Det. Robert Goren is investigating a homicide, and the medical examiner tells him that when he arrived at 6:00 p.m., the body had a temperature of 95.3 degrees Fahrenheit. By the time Nichols had arrived an hour later (at 7:00), he checks again and determines the temperature to be 94.9 degrees. The ambient air temperature is 90 degrees. Use the equation 𝑇(𝑡) = 𝑎𝑒^(−𝑘𝑡) + 90 to determine when the victim was killed. (The normal body temperature is 98.6 degrees. Round k to 3 decimal places and find the time of death to the nearest minute.
For number 1, I got -20/9, but it can't be negative so I'm confused. Thank you for answering!
Click here to see answer by Alan3354(69443)   |
Question 1069666: Det. Robert Goren is investigating a homicide, and the medical examiner tells him that when he arrived at 6:00 p.m., the body had a temperature of 95.3 degrees Fahrenheit. By the time Nichols had arrived an hour later (at 7:00), he checks again and determines the temperature to be 94.9 degrees. The ambient air temperature is 90 degrees. Use the equation 𝑇(𝑡) = 𝑎𝑒^(−𝑘𝑡) + 90 to determine when the victim was killed. (The normal body temperature is 98.6 degrees. Round k to 3 decimal places and find the time of death to the nearest minute.
I'm really confused on how to go about this problem, any help would be greatly appreciated!
Click here to see answer by KMST(5328)   |
Question 1070165: A species of animal is discovered on an island. Suppose that the population size P(t) of the species can be modeled by the following function, where time t is measured in years.
P(t) = 400/1 + 4e^-0.18t
Find the intitial population size of the species and the population size after 10 years.
Round your answers to the nearest whole number as necessary
Initial population size: ___________
Population size after 10 years: ____________
Click here to see answer by stanbon(75887)  |
Question 1070908: 1.Solve by Graphing (in Desmos) and also Solve by Substitution
y=-x^2-3x+10
y=x+5
2.After t seconds, the height, p, of a projectile (in feet) is given by the equation p(t)=-t^2+3t+2. After t seconds, the height, b, of a balloon (in feet) is given by the equation b(t)=4t-4. The projectile and the balloon are launched at the same time. After how many seconds (to the nearest hundredth) are the projectile and the balloon at the same height?
Use 𝑝(𝑡) = 𝑏(𝑡) to solve this problem
Click here to see answer by Fombitz(32388)   |
Question 1071332: The graph of a translated exponential function is shown below. Its parent function is y=4^x. If the graph is asymptotic to y=-3 and contains the points (2,-2) and (3,1), what is the equation of the function?
Click here to see answer by Boreal(15235)   |
Question 1071963: the half life of carbon14 is 5730 years.
A.) f(t)=ae^(-kt) solve for k
b.) if the bone is 65% of the original amount of carbon14. how old is the bone in years?
c.) If a bone is known to be 1900 years old, what percent of the original Carbon14 is remaining in the bone. Round to the nearest percent.
Click here to see answer by josgarithmetic(39620)  |
Question 1072026: A 15 g sample of radioactive iodine decays in such a way that the mass remaining after t
days is given by m(t) = 15e−0.087t, where m(t) is measured in grams. After how many days are there
only 5 g remaining?
Click here to see answer by ikleyn(52800)   |
Question 1072028: A certain culture initially has 25 bacteria and is observed to double every 5 hours.
A) Find an exponential model n(t) = n02t/a for the number of bacteria in the culture after t
hours.
B) Estimate the number of bacteria after 18 hours. Round down the next lower bacterium.
C) After how many hours will the bacteria count reach 2 million.
Click here to see answer by jorel1380(3719)   |
Question 1070978: A new motor boat cost $6000. The value of the boat decreases by 15% each year.
a) Write a model to describe the situation. Let V be the value of the boat after t years.
V = _(_)x
b) What is the value of the boat after 3 years? (round to two decimals)
V = $_
c) In what year is the value of the boat $2260? (round to the year)
year _
Click here to see answer by jorel1380(3719)   |
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910
|

