Tutors Answer Your Questions about Exponential-and-logarithmic-functions (FREE)
Question 118811: Good evening ma'am or sir, would you please help me on how to solve these 3 equations :
1). (ax^3)^2(ax^4)^3
2). (ab^2)^4(a^4b^2)^3
3). (5a^2xy^3)(b^3y^4)^3
Thank you very much ma'am or sir for your generosity. :)
Click here to see answer by checkley71(8403)  |
Question 120153: Please help me with this problem. I can't seem to figure out how to slove it.
Find all the zeros of each function by using synthetic division.
f(x)=3x^3-26x^2+76x-40
---I did the p/q hing to help me out, but none of them seemed to work unless I made a math error (but I would have had to do the same mistake because I did some of them twice).---
Thank You
<3KML
Click here to see answer by Edwin McCravy(20059)   |
Question 121080: Dear Algebra II tutor,
I am having trouble solving and checking thje extraneous solution of the following problem:
(2x+1)1/3 = 3
note: the 1/3 is an exponent.
I tried it out and got x=4 here is my work:
(2x+1)1/3(3) = 3(3)
2x+1=9
2x=8
x=4
I would very much appriate any help that you may offer, thank you for your time and effort.
Justin
Click here to see answer by solver91311(24713)   |
Question 125849: 4) The formula for calculating the amount of money returned for an initial deposit into a bank account or CD (certificate of deposit) is given by
A is the amount of the return.
P is the principal amount initially deposited.
r is the annual interest rate (expressed as a decimal).
n is the number of compound periods in one year.
t is the number of years.
Carry all calculations to six decimals on each intermediate step, then round the final answer to the nearest cent.
Suppose you deposit $2,000 for 5 years at a rate of 8%.
a) Calculate the return (A) if the bank compounds annually (n = 1). Round your answer to the hundredth's place.
Answer:
Show work in this space. Use ^ to indicate the power or use the Equation Editor in MS Word.
b) Calculate the return (A) if the bank compounds quarterly (n = 4). Round your answer to the hundredth's place.
Answer:
Show work in this space:
c) Does compounding annually or quarterly yield more interest? Explain why.
Answer:
Explain:
d) If a bank compounds continuously, then the formula used is
where e is a constant and equals approximately 2.7183.
Calculate A with continuous compounding. Round your answer to the hundredth's place.
Answer:
Show work in this space:
e) A commonly asked question is, “How long will it take to double my money?” At 8% interest rate and continuous compounding, what is the answer? Round your answer to the hundredth's place.
Answer:
Show work in this space:
5) Suppose that the function represents the percentage of inbound e-mail in the U.S. that is considered spam, where x is the number of years after 2000.
Carry all calculations to six decimals on each intermediate step when necessary.
a) Use this model to approximate the percentage of spam in the year 2003.
Answer:
Show your work in this space:
b) Use this model to determine in how many years (to two decimal places) it will take for the percent of spam to reach 95% provided that law enforcement regarding spammers does not change.
Answer:
Show your work in this space:
Click here to see answer by checkley71(8403)  |
Question 126487: A computer is infected with the Sasser virus. Assume that it infects 20 other computers within 5 minutes; and that these PCs and servers each infect 20 more machines within another five minutes, etc. How long until 100 million computers are infected?
Click here to see answer by scott8148(6628)   |
Question 126672: Can someone please try and solve this by 11:59pm TONIGHT!!! Or I will not receive credit at all even for trying and still getting the wrong answer!!!I can't figure this out, my friend and both got 6.88 years for part B. But my instructor says its incorrect. THANKS SO MUCH!!
A) If a bank compounds continuously, then the formula used is 
where e is a constant and equals approximately 2.7183.
Calculate A with continuous compounding. Round your answer to the hundredth's place.
Answer:
Show work in this space:
B) A commonly asked question is, “How long will it take to double my money?” At 8% interest rate and continuous compounding, what is the answer? Round your answer to the hundredth's place.
Answer:
Show work in this space:
Click here to see answer by solver91311(24713)   |
Question 127650: I was absent and my friend got my homework for me. My homework is not from the textbook and I missed the instruction. Would someone please work this problem in easy to follow steps so I can figure out how to complete the rest of my assignment? PLEASE ?
7^(2x+3)=5^(x-4)
Click here to see answer by ankor@dixie-net.com(22740)   |
Question 128256: My teacher want us to expand the following binomials. I did not understand the "easy" way and we do not have enough textbooks at my school to take one home. Please give me as much detail as you can on how to solve this type of problem 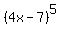
Thank you,
Click here to see answer by solver91311(24713)   |
Question 128256: My teacher want us to expand the following binomials. I did not understand the "easy" way and we do not have enough textbooks at my school to take one home. Please give me as much detail as you can on how to solve this type of problem 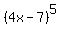
Thank you,
Click here to see answer by checkley71(8403)  |
Question 129051: If there is anyone who knows how to do this I would appreciate it if you can help me. This is due tommorrow and I am not sure where to even begin!!
Here is a question I really am lost on! I don't know what to do and am just confusing myself more. Can someone Please HelP??? In the early 1990's Iomega came out with a portable disk storage device that was capable of storing 100mb of data. There was a huge market and absolutely no competitors. For several months Iomega experienced exponential growth. If we modeled that growth using the exponential equation Growth=.05e^t where t is the number of months, then the company would double its value in 3.7 months. Unfortunately for Iomega and their shareholders, they did not realize that such growth would not continue for long. In fact, competitors began releasing their products very quickly and Iomega began experiencing logistic growth rather than exponential growth. In fact, their growth would be better modeled by the equation G=100/1+1000e^-t . This is still a nice growth, but it says that they would eventually maximize their growth at 100 times their initial size. The two groth functions intersect. That is, at some number of months .05t=G = 100/1+1000e^-t. After this time, their growth would be slower than the exponential model would predict, and eventually they would level out at a very nearly no growth. A. Your job is to find that point where the two functions intersect. You will need to use the natural log and simple algebra to solve this equation. B. How many times larger than their initial value would they be at this point? HELP!!!!!!!!!
Click here to see answer by bucky(2189)  |
Question 129339: Using matrix calculations, solve the following problem. Show Your Work.
A total of $50,000 is invested in three funds paying 6%, 8%, and 10% simple interest. The yearly interest is $3,700. Twice as much money is invested at 6% as invested at 10%. How much is invested in each of the funds.
set up the 3 linear equations in 3 variables
put the coefficients into a matrix
solve the matrix using any method you like
provide the solutions for x, y, and z.
I have two equations already which are:
.06x+.08y+.10z=3,700
x+y+z=50,000
How and where do I get the last equation? I am not really sure what to do with this problem from here. Can someone please help me. I have been at this all day. Thank you
Click here to see answer by stanbon(75887)  |
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910
|



