Question 1207302: The lengths of the sides of an equilateral triangle are log4(a), log10(b), log25(a+b) where A and B are positive numbers. What is the value of a/b?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The lengths of the sides of an equilateral triangle are log4(a), log10(b), log25(a+b)
where A and B are positive numbers. What is the value of a/b?
~~~~~~~~~~~~~~~
We are given
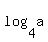 = = 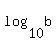 = = 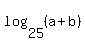 .
Let k = .
Let k = 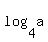 = = 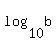 = = 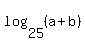 .
It means that .
It means that
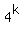 = a, (1) = a, (1)
 = b, (2) = b, (2)
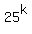 = a + b. (3)
It implies that = a + b. (3)
It implies that
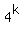 + +  = = 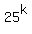 .
Divide both sides (all the terms) by .
Divide both sides (all the terms) by 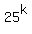 . You will get . You will get
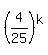 + + 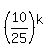 = 1,
or = 1,
or
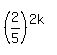 + + 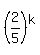 = 1. (4)
Let x = = 1. (4)
Let x = 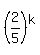 . Then equation (4) takes the form . Then equation (4) takes the form
 + x = 1,
or + x = 1,
or
 + x - 1 = 0.
Its roots are + x - 1 = 0.
Its roots are  = = 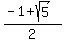 , ,  = = 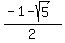 .
Our value of x is positive .
Our value of x is positive 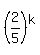 ; so, we consider only positive root x = ; so, we consider only positive root x =  .
Thus we have .
Thus we have
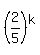 = =  ,
or ,
or
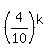 = =  .
But from (1) and (2), .
But from (1) and (2),  = = 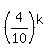 .
Thus we proved that .
Thus we proved that  = =  .
ANSWER. .
ANSWER.  = =  = 0.618033989 (approximately). = 0.618033989 (approximately).
Solved.
|
|
|