Question 984855: Find the points on inflection and discuss the concavity of the function:
f(x)=x sqrt (x+8)
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! f(x) = x * sqrt(x+8)
we will take the first derivative of f(x) and set it equal to 0 to find the points of inflection
****************************************************************************
to find the first derivative, we will use the product rule, namely
d(uv)/dx = u'v + v'u
let u = x and v = (x+8)^(1/2), then
u' = 1
v' = (1/2) * (x+8)^(-1/2)
d(uv)/dx = (x+8)^(1/2) + (x/2) * (x+2)^(-1/2)
d(uv)/dx = f'(x) = (3x + 16) / (2*(x+8)^(1/2))
****************************************************************************
the point of inflection is
(3x + 16) / (2*(x+8)^(1/2)) = 0
3x + 16 = 0
x = -16 / 3
****************************************************************************
the x axis intercepts for f(x) are
f(x) = 0 = x * sqrt(x+8)
x = 0 and x = -8
****************************************************************************
In order to discuss concavity of f(x), we calculate the second derivative of f(x), we do this by starting with f'(x) and taking its derivative
f'(x) = (3x + 16) / (2*(x+8)^(1/2))
to take this derivative, we use the quotient rule, namely
d(u/v)/dx = (u'v - uv') / v^2
u = (3x + 16)
v = (2 *(x+8)^(-1/2))
u' = 3
******************************************************************************
for v' we use the product rule
u = 2
v = (x+8)^(-1/2)
v' = 0 + (2 * (x+8)^(-3/2) / -2
v' = -(x+8)^(-3/2)
*****************************************************************************
d(u/v)/dx = f''(x) = (3*(2 *(x+8)^(-1/2))) + ((3x + 16)*(x+8)^(-3/2)) / (4*(x+8))
f''(x) = (3x + 32) / (4*(x+8)^(3/2))
to discuss concavity, we evaluate f''(x) on the interval (-8, +infinity)
note that for x < -8, f(x) is imaginary
*****************************************************************************
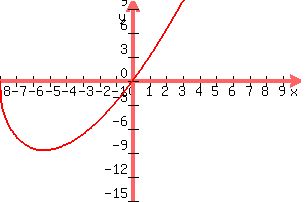
from inspection we see that f''(x) is positive on (-8, infinity) which means that f(x) is concave up on that interval, here is the graph of f(x)
|
|
|